安宜高级中学2006-2007学年度第一学期高三数学函数练习(A卷)
注意:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、函数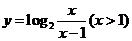 的反函数是
的反函数是
A.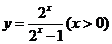 B.
B.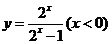 C.
C.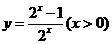 D.
D.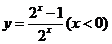
2、函数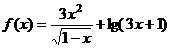 的定义域是
的定义域是
A.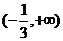 B.
B. 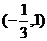 C.
C. 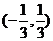 D.
D.
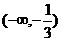
3、下列大小关系正确的是
A.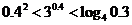 ; B.
; B.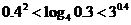 ;
;
C.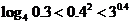 ; D.
; D.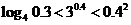
4、下列函数中,在其定义域内既是奇函数又是减函数的是
A. 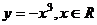 B.
B. 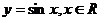 C.
C. 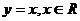 D.
D. 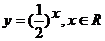
5、设函数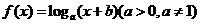 的图像过点
的图像过点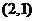 ,其反函数的图像过点
,其反函数的图像过点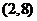 ,则
,则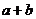 等于
等于
A.3 B
6、若函数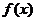 是定义在R上的偶函数,在
是定义在R上的偶函数,在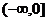 上是减函数,且
上是减函数,且 ,则使得
,则使得 的x的取值范围是
的x的取值范围是
A.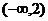 B.
B.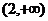 C.
C.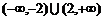 D.(-2,2)
D.(-2,2)
7、在R上定义运算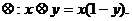 若不等式
若不等式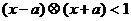 对任意实数
对任意实数 成立,则
成立,则
A.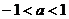 B.
B.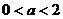 C.
C.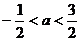 D.
D.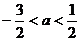
8、为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接收方由密文
密文(加密),接收方由密文 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文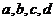 对应密文
对应密文 例如,明文
例如,明文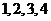 对应密文
对应密文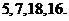 当接收方收到密文
当接收方收到密文 时,则解密得到的明文为A.
时,则解密得到的明文为A.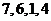 B.
B.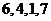 C.
C.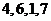 D.
D.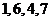
9、函数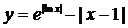 的图象大致是
的图象大致是
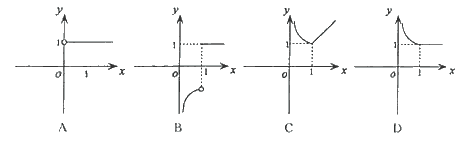
10、设f(x)是定义在R上以6为周期的函数,f(x)在(0,3)内单调递增,且y=f(x)的图象关于直线x=3对称,则下面正确的结论是
A. f(6.5)<f(3.5)<f(1.5) B. f(3.5)<f(1.5)<f(6.5)
C. f(6.5)<f(1.5)<f(3.5) D. f(3.5)<f(6.5)<f(1.5)
第Ⅱ卷 选择题(满分100分)
二、填空题:本大题共6小题,每小题5分,共30分。把答案填写在答题卡相应位置上。
11、方程 的解集是
的解集是
12、已知a,b为常数,若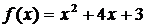 ,
, ,则
,则 _________。
_________。
13、若函数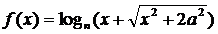 是奇函数,则a=
.
是奇函数,则a=
.
14、函数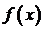 对于任意实数
对于任意实数 满足条件
满足条件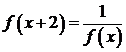 ,若
,若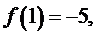 则
则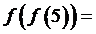 __________。
__________。
15、设函数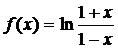 ,则函数
,则函数 的定义域为__________
的定义域为__________
16、设函数f(x)的图象关于点(1,2)对称,且存在反函数f-1(x),f (4)=0,则f-1(4)= .
三、解答题:本大题共5小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17、设函数 的定义域为集合M,函数
的定义域为集合M,函数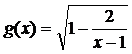 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合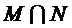 ,
,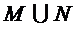 .
.
18、设函数 .
.
(1)在区间 上画出函数
上画出函数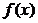 的图像;
的图像;
(2)设集合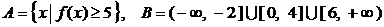 . 试判断集合
. 试判断集合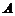 和
和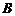 之间的关系,并给出证明;
之间的关系,并给出证明;
19、已知二次函数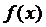 的二次项系数为a,且不等式
的二次项系数为a,且不等式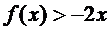 的解集为(1,3).
的解集为(1,3).
(1)若方程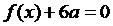 有两个相等的根,求
有两个相等的根,求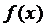 的解析式;
的解析式;
(2)若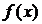 的最大值为正数,求a的取值范围.
的最大值为正数,求a的取值范围.
20、已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
21、已知a为实数,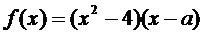
(Ⅰ)求导数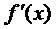 ;
;
(Ⅱ)若 ,求
,求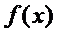 在[--2,2] 上的最大值和最小值;
在[--2,2] 上的最大值和最小值;
(Ⅲ)若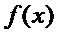 在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
 安宜高级中学2006-2007学年度第一学期
安宜高级中学2006-2007学年度第一学期
高三数学答题卡
第Ⅰ卷 选择题 (共50分)
题号
1
2
3
4
5
6
7
8
9
10
得分
答案
第Ⅱ卷 非选择题 (共100分)
11题 12题
13题 14题
15题 16题
17题解:
三、解答题
 18题解:
18题解:
19题解:
20题解:
21题解:
ABCACDCCDB
 2
2 

(2,1)È(1,2) -2
17、解:(Ⅰ)

(Ⅱ)

 18、[解](1)
18、[解](1)
(2)方程 的解分别是
的解分别是 和
和 ,由于
,由于 在
在 和
和 上单调递减,在
上单调递减,在 和
和 上单调递增,因此
上单调递增,因此
 .
.
由于 .
.
19、解:(Ⅰ)

 ①
①
由方程 ②
②
因为方程②有两个相等的根,所以 ,
,
即 
由于 代入①得
代入①得 的解析式
的解析式

(Ⅱ)由
及
由 解得
解得 
故当 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是
20、解:(Ⅰ)设函数 的图象上任意一点
的图象上任意一点 关于原点的对称点为
关于原点的对称点为 ,则
,则

∵点 在函数
在函数 的图象上
的图象上
∴
(Ⅱ)由
当 时,
时, ,此时不等式无解
,此时不等式无解
当 时,
时, ,解得
,解得

因此,原不等式的解集为

21、解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
得 ,此时有
,此时有 .
.
由 得
得 或x=-1 , 又
或x=-1 , 又
所以f(x)在[--2,2]上的最大值为 最小值为
最小值为
(Ⅲ)解法一:  的图象为开口向上且过点(0,--4)的抛物线,由条件得
的图象为开口向上且过点(0,--4)的抛物线,由条件得

即 ∴--2≤a≤2.
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令 即
即 由求根公式得:
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时,  ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得: --2≤a≤2.
解不等式组得: --2≤a≤2.
∴a的取值范围是[--2,2].