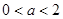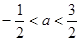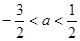摘要:在R上定义运算若不等式对任意实数成立.则
网址:http://m.1010jiajiao.com/timu_id_21355[举报]
ABCACDCCDB
 2
2 

(2,1)È(1,2) -2
17、解:(Ⅰ)

(Ⅱ)

 18、[解](1)
18、[解](1)
(2)方程 的解分别是
的解分别是 和
和 ,由于
,由于 在
在 和
和 上单调递减,在
上单调递减,在 和
和 上单调递增,因此
上单调递增,因此
 .
.
由于 .
.
19、解:(Ⅰ)

 ①
①
由方程 ②
②
因为方程②有两个相等的根,所以 ,
,
即 
由于 代入①得
代入①得 的解析式
的解析式

(Ⅱ)由
及
由 解得
解得 
故当 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是
20、解:(Ⅰ)设函数 的图象上任意一点
的图象上任意一点 关于原点的对称点为
关于原点的对称点为 ,则
,则

∵点 在函数
在函数 的图象上
的图象上
∴
(Ⅱ)由
当 时,
时, ,此时不等式无解
,此时不等式无解
当 时,
时, ,解得
,解得

因此,原不等式的解集为

21、解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
得 ,此时有
,此时有 .
.
由 得
得 或x=-1 , 又
或x=-1 , 又
所以f(x)在[--2,2]上的最大值为 最小值为
最小值为
(Ⅲ)解法一:  的图象为开口向上且过点(0,--4)的抛物线,由条件得
的图象为开口向上且过点(0,--4)的抛物线,由条件得

即 ∴--2≤a≤2.
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令 即
即 由求根公式得:
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时,  ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得: --2≤a≤2.
解不等式组得: --2≤a≤2.
∴a的取值范围是[--2,2].
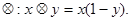 若不等式
若不等式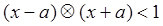 对任意实数
对任意实数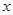 成立,则( )
成立,则( ) 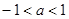 B.
B.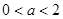
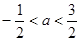 D.
D.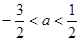
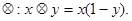 若不等式
若不等式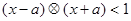 对任意实数
对任意实数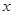 成则
成则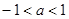 B.
B.
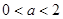
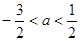 D.
D.
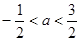
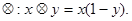 若不等式
若不等式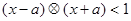 对
对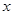 成立, 则( )
成立, 则( )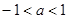 B.
B.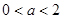 C.
C.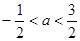 D.
D.
 若不等式
若不等式 对任意实数
对任意实数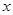 成立,则( )
成立,则( )