-
1.设集合M={
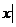 x<5},N={
x<5},N={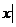 x>3},那么“{
x>3},那么“{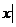 x
x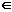 M或x
M或x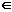 N}是“x∈M
N}是“x∈M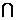 N”的
( )
N”的
( )A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分条件又非必要条件
联想:(1)α≠
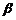 是sinα≠sin
是sinα≠sin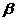 的
的A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
(2)函数f (x) 的导函数f′(x) >0是f(x)单调递增的( )
A.必要非充分条件 B.充分非必要条件
C.充要条件 D.既非充分又非必要条件
(3)下列给出四个命题:
① 对于实数m和向量
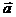 ,
,
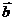 ,恒有:m(
,恒有:m(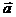 -
-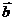 )=m
)=m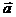 -n
-n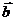 ; ②对于实数m,n和向量
; ②对于实数m,n和向量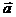 ,恒有:(m-n)
,恒有:(m-n)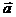 =m
=m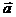 -n
-n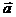 ; ③若m
; ③若m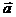 =m
=m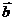 (m
(m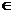 R),则:
R),则: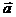 =
=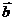 ; ④若m
; ④若m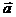 =n
=n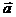 (m,n
(m,n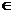 R,
R, 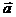 ≠
≠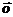 ),则m=n。其中正确命题的个数是(
)
),则m=n。其中正确命题的个数是(
)A.1 B.2 C.3 D.4
-
2.已知偶函数y=loga
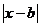 在(-
在(-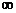 ,0)上递增,则a、b分别满足( )
,0)上递增,则a、b分别满足( )A.a>1, b>0 B.a>1,b
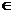 R
C.0<a<1,b=0 D.a>1,b=0
R
C.0<a<1,b=0 D.a>1,b=0联想:(1)函数y=f(x)=log
 (2x+1)在(-
(2x+1)在(-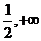 )上是单调递增函数,则实数a的取值范围是___________________.
)上是单调递增函数,则实数a的取值范围是___________________.(2)已知函数f(x)=loga(x-k)的图象过点(4,0),又反函数的图象过点(1,7),则f(x)是( )
A.增函数 B.减函数 C.奇函数 D.偶函数
(3)已知f-1(x)是f(x)的反函数,f(x)过点(4,1),则f-1(x+3)必过点
A.(1,4) B.(4,-2) C.(-2,4) D.(4,1)
(4)函数f(x)=a+bx-1(b>0且b≠1)的图象过点(1,3),f-1(x+a)(x>0)的图象过点(4,2),则
f-1(x)=_______________________.
-
3.函数y=sin(2x-1)的图象由y=sin(2x+1)的图象怎样变化而得到?( )
A.向左平移2个单位 B.向右平移2个单位
C.向左平移1个单位
 D.向右平移1个单位
D.向右平移1个单位
联想:(1)已知f(x)=sin(x+
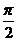 ),g(x)=cos(
),g(x)=cos(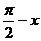 ),则f(x)的图象( )
),则f(x)的图象( )A.与g(x)的图象相同 B.与g(x)的图象关于y轴的对称

C. 是由g(x)的图象向左平移
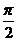 个单位得到的.
个单位得到的.D. 是由g(x)的图象向右平移
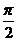 个单位得到的.
个单位得到的.(2)要想得到y=2sin2x的图象,只需要把函数y=4sin(x+
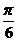 ) cos(x+
) cos(x+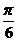 )的图象(
)
)的图象(
)A.向左平移
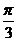 个单位
B.向右平移
个单位
B.向右平移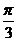 个单位
个单位 C.向左平移
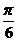 个单位
D.向右平移
个单位
D.向右平移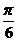 个单位
个单位(3) 要得到y=cos(2x+
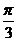 )的图象,只需把y=sin(2x-
)的图象,只需把y=sin(2x-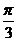 )的图象向____________ 平移_________ 而得到.
)的图象向____________ 平移_________ 而得到. -
4.设(5x
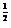 -x
-x )n的展开式的各项系数之和为M,而二项式系数之和为N,且M-N=992。则展开式中x2项的系数为(
)
)n的展开式的各项系数之和为M,而二项式系数之和为N,且M-N=992。则展开式中x2项的系数为(
)A.250 B.-250 C.150 D.-150
联想:(1)已知(1-2x)6=a0+a1x+a2x2+------+a6x6,则
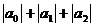 +…+
+…+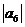 的值( )
的值( )A.1 B.26 C.35 D.36
(2)设(2x+
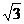 )
)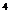 =a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为(
)
=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为(
)A.2 B.-2 C.1 D.-1
(3)已知(x+xlgx)5展开式中第3项为106,则x的值为( )
A.10 B.100 C.10或10
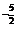 D.10
D.10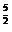
(4)若(x+
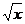 )n的展开式中第三项系数为36,则自然数n的值为_____________.
)n的展开式中第三项系数为36,则自然数n的值为_____________. -
5.直线
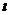 与平面α内共点的三条直线a、b、c分别成等角,那么
与平面α内共点的三条直线a、b、c分别成等角,那么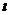 与平面α所成的角为( )
与平面α所成的角为( )A.
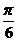 B.
B.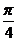 C.
C.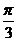 D.
D.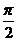
联想:(1)三条两两异面直线,且两两成角相等,这三条直线与平面α都平行,则它们所成的角为_______________.
(2) 两条异面直线a、b所成的角为
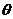 ,过空间一定点P的直线
,过空间一定点P的直线 有且仅有三条与a、b所成的角为750,则a与b所成的角为_______________.
有且仅有三条与a、b所成的角为750,则a与b所成的角为_______________. -
6.
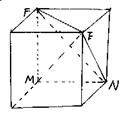 如图,E,F,M,N是正方体的四个顶点,记d1为F到面FMN的距离,d2为E面EMN的距离,d3为M到面EFN的距离,那么d1,d2,d3的大小关系为(
)
如图,E,F,M,N是正方体的四个顶点,记d1为F到面FMN的距离,d2为E面EMN的距离,d3为M到面EFN的距离,那么d1,d2,d3的大小关系为(
)A.d1<d2<d3 B.d2<d3<d1
C.d2<d1<d3 D.d3<d2<d1
联想:(1)三棱柱ABC-A1B1C1的体积为V,P、Q分别为AA1、CC1上的点,而且满足PA=QC1,则VB-APQC=( )
A.
 B.
B.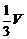 C.
C.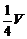 D.
D.
 (2)如图,多面体ABCDFE中,ABCD是边长为3的正方形,EF∥平面ABCD,EF=
(2)如图,多面体ABCDFE中,ABCD是边长为3的正方形,EF∥平面ABCD,EF=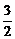 ,EF到面ABCD的距离为2,则多面体的体积为(
)
,EF到面ABCD的距离为2,则多面体的体积为(
)A.
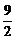 B.5 C.6
D.
B.5 C.6
D.
-
7.光线从点P(2,3)射到直线y=-x-1上,反射后经点 Q(1,1),则反射光线方程为( )
A.x-y+1=0 B.4x-5y+31=0 C.4x-5y+16=0 D.4x-5y+1=0
联想:(1)光线x-2y+5=0遇到直线3x-2y+7=0即行反射,光线与反射光线所夹角是( )
A.2arctan
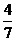 B.
B. C.2 arctan
C.2 arctan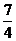 D.
D.
(2)如图 光线从点P(1,3)入射到y轴后即行反射,射到x轴上再即行反射,最后一次的反射光线经过点Q(5,2),则第一次反射光线方程为____________________.
-
8.若x
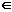 [0,3]时,不等式a≥x2-2x-1恒成立,则实数a的最小值是(
)
[0,3]时,不等式a≥x2-2x-1恒成立,则实数a的最小值是(
)A.-2 B.2 C.-1 D.不存在
联想:若ax+2≥20x-x2在(0,+
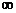 )恒成立,则实数a的取值范围是
。
)恒成立,则实数a的取值范围是
。 -
9.在A.P{an}中,a1+a3=4,a4+a6= -2,如果an=log3bn,则
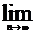 (
(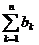 )=
。
)=
。联想:等差数列{
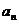 }中,a1-a4+a6+a10-a12+a15=2,则前15项的和为S15=( )
}中,a1-a4+a6+a10-a12+a15=2,则前15项的和为S15=( )A.-15 B.15 C.-30 D.30
-
10.正方体的8个顶点中, 任何两点的连线中有 对异面直线。
联想:(1)某市要组成一支有12名运动员的篮球队,这些队员要从7所不同的学校选出,每校至少一人,则有 种不同的选派方案。
(2)某仪表显示屏上排有七个小孔,每个小孔可显示出0或1,若每次显示其中三个孔,但相邻两个孔不能同时显示,则这个显示屏可以显示的不同信号的种数是 。
-
11.椭圆的一个焦点为圆心,焦距为半径的圆过椭圆的两个顶点,则此椭圆的离心率e= 。
联想:(1)双曲线
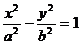 中,左焦点为F,右顶点为A,虚轴顶点为B,若BF⊥AB,则离心率e=
。
中,左焦点为F,右顶点为A,虚轴顶点为B,若BF⊥AB,则离心率e=
。(2)椭圆
 (a>b>0)的两个顶点A(a,0),B(0,b),若右焦点F到直线AB的距离为
(a>b>0)的两个顶点A(a,0),B(0,b),若右焦点F到直线AB的距离为 ,则离心率e=
。
,则离心率e=
。 -
12.某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需过滤的次数为( )
A.5 B.10 C.14 D.15
联想:某公司一月份推出新产品A,成本为400元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x元/件)
650
662
719
800
900
销售量(y件)
350
338
281
200
100
据此,写出x与y可满足的一个函数关系式 ;
 并据此,应将销售价定为
元时,利润最大。
并据此,应将销售价定为
元时,利润最大。 -
13.袋内有9个白球和3个红球,从袋内任意地顺次取出三个球(取出后不放回)。
(I)求第三次取出的球是白球的概率
(II)当第三次取出的球是白球时,问第一次取出的球是白球的概率是多少?
联想:如图,已知电路中4个开关闭合的概率都是
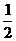 ,
,且是相互独立的,求灯亮的概率。
-
14.设数列{an}的前n项和为Sn,且a2≠a1,证明:{an}是首项为1的等比数列的充要条件是存在非零常数a,b满足Sn=a+ban且a+b=1
联想:数列{an}中,其前n项和为Sn,当n≥1时,Sn+1是an+1与Sn+1+k的等比中项(k≠0)
(I)求证:对于n≥1有
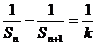
(II)设a1=
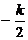 ,求Sn的表达式。
,求Sn的表达式。(III)设a1=
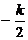 ,且{
,且{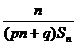 }成等差数列,求证:
}成等差数列,求证: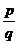 是与k无关的常数。
是与k无关的常数。联想与激活(2)
-
1.函数f (x)=log0.5(sinxcosx)的单调递减区间是(以下k∈Z)( )
A.(k
 -
-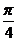 ,k
,k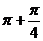 )
B.
)
B.
C.
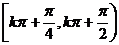 D.
D.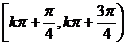
联想:(1)函数y=cos(
 )
)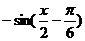 的单调递增区间为( )
的单调递增区间为( )A.[4
 ]
B.[
]
B.[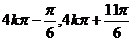 ]
] C.[
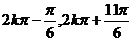 ]
D.[
]
D.[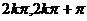 ] (以上k∈Z)
] (以上k∈Z)(2)函数f (x)=lg(sinx-cosx)的单调递减区间为 。
-
2.函数f (x)=
 的最小正周期为(
)
的最小正周期为(
)A.2
 B.
B. C.
C.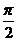 D.以上都不对
D.以上都不对联想:(1)函数f (x)=sin(
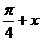 ).cos(
).cos(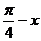 )的最小周期为( )
)的最小周期为( )A.
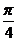 B.
B.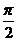 C.
C. D.2
D.2
(2)函数y=sin6x+cos6x的最小正周期为 。
(3)函数y=tan
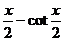 的最小正周期为 。
的最小正周期为 。(4)已知函数f (x)是以2为周期的偶函数且当x∈(0,1)时,f (x)=x+1,则f (x)在(1,2)上的解析式是( )
A.f (x)=1-x B.f (x)=3-x C.f (x)=x-3 D.f (x)=-x-1
-
3.设sin (α+2β)=5sinα,则tan(α+β):tanβ= 。
联想:(1)已知:tan(α+β) =4,tan(α-β)=2,那么tan2α= .
(2)
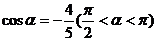 ,tan
,tan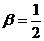 ,则
,则 之值为
。
之值为
。(3)已知:
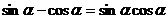 ,则
,则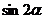 的值为( )
的值为( )A.
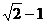 B.
B.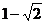 C.
C.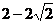 D.
D.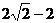
(4)在△ABC中,若sinA=
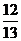 ,cosB=
,cosB=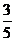 ,则cosC的值为(
)
,则cosC的值为(
)A.
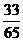 B.
B.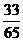 或
或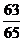 C.-
C.-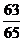 D.-
D.-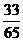 或-
或-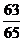 4.不等式(
4.不等式(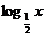 )2<
)2<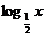 2的解集为
.
2的解集为
.联想(1)不等式
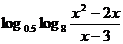 <0的解集为
.
<0的解集为
.(2)不等式
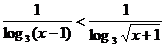 的解集为( )
的解集为( )A.(3,+∞) B.(0,3) C.(1,2) D.(1,2)∪(3,+∞)
(3)已知定义在R上的偶函数f (x)在x∈
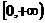 上是增函数,且f (
上是增函数,且f (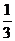 )=0,则满足f (
)=0,则满足f (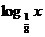 )>0的x的取值范围是( )
)>0的x的取值范围是( )A.
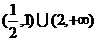 B.
B.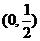 C.
C.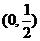
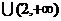 D.
D.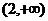
(4)不等式
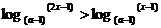 成立的充要条件是( )
成立的充要条件是( )A.a>2,x>1 B.a>1,x>1 C.a>2,x>0 D.x>0
-
5.如果平面α外的两条异面直线a、b在平面α上的射影是两条平行直线,那么直线a、b与平面α的位置关系是( )
A.仅有一条直线与平面α相交 B.两条直线都与平面相交
C.两条直线都与平面α相交 D.至少有一条直线与平面α相交
联想:(1)P为异面直线a、b外任一点,过P与a、b都平行的平面有( )
A.唯一一个 B.恰好两个 C.至多一个 D.至少一个
(2)过平面外一直线作该平面的平行平面( )
A.只可能作一个 B.至少作一个 C.至多作一个 D.这样的平面不存在
(3)a、b是两异面直线,下列结论正确的是 ( )
A.过不在a、b上的任一点,可作一个平面与a、b都平行
B.过不在a、b上的任一点,可作一条直线与a、b都相交
C.过不在a、b上的任一点,可作一条直线与a、b都平行
D.过a可以并且只可以作一个平面与b平行
-
6.给出4个命题:
①到两定点距离之和为常数的动点的轨迹是椭圆;
②到两个定点的距离之差的绝对值为常数的点的轨迹是双曲线;
③到定直线x=
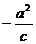 和定点F(-c,0)的距离之比为
和定点F(-c,0)的距离之比为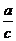 (c > a >0)的点的轨迹是双曲线;
(c > a >0)的点的轨迹是双曲线;④到定点F(c,0)和定直线x=
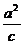 的距离之比为
的距离之比为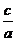 (a
> c>0)的动点轨迹是椭圆;
(a
> c>0)的动点轨迹是椭圆;请将正确命题的代号都填在横线上 。
联想:(1)抛物线y2 = 4x的焦点为F,准线交x轴于R点,过抛物线上一点P(4,4)作PQ⊥
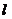 于Q,则梯形PQRF的面积是
( )
于Q,则梯形PQRF的面积是
( )A.12 B.14 C.16 D.18
(2)过椭圆
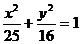 左焦点F的直线交椭圆于A、B两点
左焦点F的直线交椭圆于A、B两点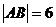 过A、B分别作左准线
过A、B分别作左准线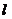 的垂线AA1⊥
的垂线AA1⊥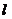 于A1,BB1⊥
于A1,BB1⊥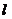 于B1,以
于B1,以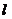 轴将椭圆在空中旋转1200,则线段AB所扫过的曲面面积为
。
轴将椭圆在空中旋转1200,则线段AB所扫过的曲面面积为
。(3)已知点A(3,2),F(2,0),在双曲线
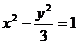 上求一点P,其坐标为
时,
上求一点P,其坐标为
时,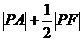 的值最小。
的值最小。 -
7.已知正六棱锥的侧面与底面所成的角为α,侧棱与底面所成的角为β,则tanβ.cotα的值为 ( )
A.
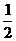 B.
B.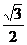 C.
C.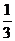 D.
D.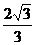
联想:(1)已知三棱锥P-ABC中,∠APB=∠BPC=∠CPA=900三棱锥侧面与底面所成的角分别为α1,α2,α3,则下列各式中正确的是 ( )
A.sinα1sinα2sinα3=
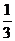 B.sin2α1+sin2α2+sin2α3=1
B.sin2α1+sin2α2+sin2α3=1C.cosα1cosα2cosα3=
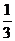 D.cos2α1+cos2α2+cos2α3=1
D.cos2α1+cos2α2+cos2α3=1(2)正三棱锥的侧棱长是底面边长的k倍,则k的取值范围是 ( )
A.(0,+∞) B.(
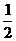 ,+∞) C.(
,+∞) C.(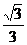 ,+∞) D.[
,+∞) D.[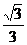 ,+∞]
,+∞](3)正四棱锥P-ABCD的棱长均为a,点E是分PA为1:2的内分点,F和G分别是分EB和ED的比为2:1的内分点,则异面直线PC和FG所成角是 ( )
A.
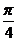 B.
B.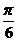 C.
C.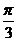 D.
D.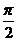
(4)正方体AC1中,E,F分别为棱AB,C1D1的中点,则A1B1与截面A1ECF所成角的正弦值为 。
(5)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角为 ( )
A.
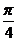 B.
B.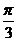 C.
C.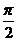 D.不确定
D.不确定 -
8.数11100-1的末尾连续的零的个数是 ( )
A.0 B.3 C.5 D.7
联想:(1)①2300除以9的余数为 ,②8788+8被88除所得余数为 。
(2)计算某项税率,需用公式y = ( 1- 5x)n(n
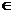 N+)。现已知y的展开式中各项的二项式系数之和为64,用四舍五入的方法计算x =
N+)。现已知y的展开式中各项的二项式系数之和为64,用四舍五入的方法计算x = 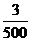 时,y的值,若精确到0.001,其千分位上的数字应是
( )
时,y的值,若精确到0.001,其千分位上的数字应是
( )A.5 B.4 C.3 D.2
-
9.已知某企业的总收入函数为R=26x-2x2-4x3,总成本函数C = 8x+x2,其中x表示产品的产量,求企业获得最大利润时的产量为 ,最大利润为 。
联想:用边长为48cm的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为 ( )
A.6 B.8 C.10 D.12
-
10.设圆x2 + y2 = 4和直线y = x + a相交于A,B两点,这时
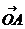 .
.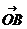 = 其中O是坐标原点,又当两个向量的夹角为300时,a的值为
。
= 其中O是坐标原点,又当两个向量的夹角为300时,a的值为
。联想:(1)在原点为O的直角坐标平面上,有以点A(4,-3)为直角顶点的Rt△AOB,已知AB的长为OA长的2倍,且点B的纵坐标为正,则
①向量
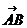 为
。
为
。②A点关于直线OB的对称点的坐标为 。
(2)已知:
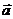 = (cosα,sinα),
= (cosα,sinα), 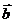 = (cosβ,sinβ),且
= (cosβ,sinβ),且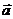 与
与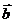 不共线,
不共线,(Ⅰ)
 与
与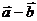 的夹角为
。
的夹角为
。(Ⅱ)若
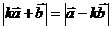 ,且0<α<β<π,k
,且0<α<β<π,k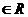 且k ≠0,则β-α的值为 。
且k ≠0,则β-α的值为 。(3)若将向量
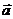 =(2,1)围绕原点按逆时针方向旋转
=(2,1)围绕原点按逆时针方向旋转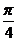 得到向量
得到向量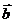 ,则向量
,则向量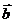 =
=。
-
11.已知函数f(x)=x4 + (a-2) x2 +(5-a)对任意实数x恒为正值,求实数a的取值范围。
联想:(1)设f ( x) = x2-2ax+2,当x
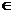
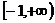 时,f ( x )≥a恒成立,求实数a的取值范围。
时,f ( x )≥a恒成立,求实数a的取值范围。(2)设函数
 与
与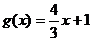 ,若恒有f ( x )≤g
( x )成立,试求实数a的取值范围。
,若恒有f ( x )≤g
( x )成立,试求实数a的取值范围。(3)已知函数
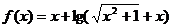 ,若不等式f ( m . 3x ) + f ( 3x-9x-2 ) < 0,对任意
,若不等式f ( m . 3x ) + f ( 3x-9x-2 ) < 0,对任意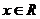 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。 -
12.
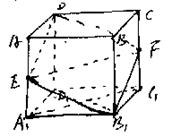 正四棱柱ABCD-A1B1C1D1中,底面边长为
正四棱柱ABCD-A1B1C1D1中,底面边长为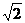 ,侧棱长为
,侧棱长为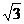 ,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C。
,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C。联想:直四棱柱ABCD-A1B1C1D1的底面是菱形,AD=AA1=a,∠DAB=600,E,F为AA1,CC1的中点。
(Ⅰ)证明:面B1EF⊥平面BDD1;(Ⅱ)求直四棱
柱被面DEB1F所截得的下半部分的体积;
(Ⅲ)求面DEB1F与底面A1B1C1D1所成的二面角。
-
13.两个数列{an}和{bn}满足
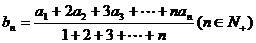
(1)若数列{bn}是等差数列,求证:数列{an}也是等差数列。
(2)试问(1)的逆命题是否成立?若成立,给出证明;若不成立,说明理由。