18.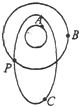 如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
 如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做匀速圆周运动轨道半径为r的卫星,C为绕地球沿椭圆轨道运动的卫星,长轴大小为a,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期相同,下列说法正确的是( )| A. | 物体A的线速度小于卫星B的线速度 | |
| B. | 卫星B离地面的高度可以为任意值 | |
| C. | a与r长度关系满足a=2r | |
| D. | 若已知物体A的周期和万有引力常量,可求出地球的平均密度 |
17.如图所示,汽车通过一陡坡,若汽车匀速率的由坡底A运动到坡顶B,则下列说法正确的是( )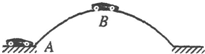

| A. | 汽车的机械能守恒 | |
| B. | 重力的瞬时功率恒定不变 | |
| C. | 合力对汽车做正功 | |
| D. | 汽车牵引力做的功等于克服阻力和重力做的总功 |
16.两颗靠得很近的天体称为双星,它们都绕两者连线上某点为圆心做匀速圆周运动,因而不至于由于万有引力而吸引到一起,则以下说法中正确的是( )
| A. | 它们做圆周运动所需要的向心力由太阳对它们的引力提供 | |
| B. | 它们中质量较大的星的向心力较大 | |
| C. | 它们做圆周运动的线速度大小之比与其质量成反比 | |
| D. | 它们做圆周运动的角速度之比与其质量成反比 |
15.甲乙两质点在同一直线上运动,甲质点所受的合力F随时间变化的规律如图甲所示;乙质点速度v随时间变化的规律如图乙所示.(取向右为正方向)已知t=0时两质点的速度均为零,下列说法中正确的是( )


| A. | t1到t2时间内,甲乙两质点加速度方向相同 | |
| B. | t2时刻甲速度最大,乙位移最大 | |
| C. | t1到t4时时间内,甲质点先向右运动,再向左运动 | |
| D. | t4时刻,乙离出发点最远 |
14.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 开普勒利用自己长期观测的数据发现了行星运动的规律 | |
| B. | 牛顿利用自己发现的万有引力定律首次测出了地球的质量 | |
| C. | 库仑利用扭秤实验测出了元电荷的电荷量 | |
| D. | 法拉第提出了电场的概念并用电场线来形象的描述电场的分布情况 |
13.某人造卫星绕地球做匀速圆周运动,它离地面的高度为2R,R为地球半径.已知地球表面的重力加速度为g,引力常量为G,求:
(1)地球的质量M;
(2)卫星的向心加速度大小;
(3)地球的第一宇宙速度大小.
(1)地球的质量M;
(2)卫星的向心加速度大小;
(3)地球的第一宇宙速度大小.
11.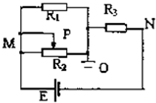 如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
 如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )| A. | 都升高 | |
| B. | 都降低 | |
| C. | M点电势升高,N点电势降低 | |
| D. | M点电势的改变量大于N点电势的改变量 |
10.关于电源与电动势的下列说法,正确的是( )
| A. | 当外电路的电阻变化时,电源的电动势一定保持不变 | |
| B. | 电源可以通过静电力做功,把其他形式的能转化成电势能 | |
| C. | 电源的电动势大小与电源的体积有关 | |
| D. | 由于电源内部具有电阻,因此电源内部也有电压 |
9.登月飞船绕月球表面做匀速圆周运动的线速度为v;飞船在月球表面上降落后,宇航员用弹簧测力计测量一质量为m的物体的重力,物体静止时,弹簧测力计的示数为F.万有引力常量为G,则月球的质量为( )
0 148305 148313 148319 148323 148329 148331 148335 148341 148343 148349 148355 148359 148361 148365 148371 148373 148379 148383 148385 148389 148391 148395 148397 148399 148400 148401 148403 148404 148405 148407 148409 148413 148415 148419 148421 148425 148431 148433 148439 148443 148445 148449 148455 148461 148463 148469 148473 148475 148481 148485 148491 148499 176998
| A. | $\frac{{m{v^2}}}{GF}$ | B. | $\frac{{F{v^2}}}{Gm}$ | C. | $\frac{{F{v^4}}}{Gm}$ | D. | $\frac{{m{v^4}}}{GF}$ |
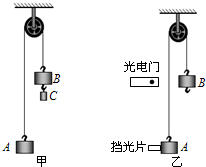 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.