3．如图所示是某弹簧振子的振动图象，由图可知（ ）
| A． | 质点的振幅是5cm，周期是2s | |
| B． | 在t=1.5s时，质点的速度和加速度方向相同 | |
| C． | 在t=1.0s时，质点的位移最大，速度为零，加速度-x方向最大 | |
| D． | 在t=4.0s时，质点的速度为零 |
2．
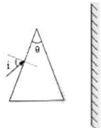如图所示某三棱镜的顶角θ=41°27′，几种单色光的折射率n如表所示．一束白光以较大的入射角通过棱镜后，在光屏上形成从紫到红的彩色光带，当入射角i渐减小到零的过程中，屏上彩色光带的变化情况是（ ）（$\frac{1}{sin41°27′}$=1.516）
如图所示某三棱镜的顶角θ=41°27′，几种单色光的折射率n如表所示．一束白光以较大的入射角通过棱镜后，在光屏上形成从紫到红的彩色光带，当入射角i渐减小到零的过程中，屏上彩色光带的变化情况是（ ）（$\frac{1}{sin41°27′}$=1.516）| 紫 | 蓝 | 绿 | 黄 | 橙 | 红 | |
| n | 1.532 | 1.528 | 1.519 | 1.517 | 1.514 | 1.512 |
| A． | 紫光最先消失，红光最后消失 | B． | 紫光最先消失，黄光最后消失 | ||
| C． | 红光最先消失，紫光最后消失 | D． | 红光最先消失，橙光最后消失 |
1．
如图所示电路中，线圈L与灯泡A并联，当合上开关S后灯A正常发光．已知，线圈L的电阻小于灯泡A的电阻．则下列现象可能发生的是（ ）
如图所示电路中，线圈L与灯泡A并联，当合上开关S后灯A正常发光．已知，线圈L的电阻小于灯泡A的电阻．则下列现象可能发生的是（ ）| A． | 闭合S时，灯泡A慢慢变亮 | |
| B． | 当断开S时，灯泡A立即熄灭 | |
| C． | 当断开S时，灯泡A突然闪亮一下，然后逐渐熄灭 | |
| D． | 若把线圈L换成电阻，断开S时，灯泡A突然闪亮一下，然后逐渐熄灭 |
20．
如图所示是双缝干涉实验装置的示意图，S为单缝，S1、S2为双缝，P为光屏．用绿光从左边照射单缝S时，可在光屏P上观察到干涉条纹，下列说法正确的是（ ）
如图所示是双缝干涉实验装置的示意图，S为单缝，S1、S2为双缝，P为光屏．用绿光从左边照射单缝S时，可在光屏P上观察到干涉条纹，下列说法正确的是（ ）| A． | 减小双缝间的距离，干涉条纹间的距离增大 | |
| B． | 增大双缝到屏的距离，干涉条纹间的距离减小 | |
| C． | 将绿光换为红光，干涉条纹间的距离减小 | |
| D． | 将绿光换为紫光，干涉条纹间的距离增大 |
真空中有一等腰梯形匀强磁场区域ABCD，磁场方向垂直纸面向里，强度为B，且AD=AB=a，BC=2a，如图所示，建立沿DA边为x轴A为原点的直角坐标系，从A点在纸面内沿y轴正方向发射各种速率的电子，设电子间相互作用忽略，已知电子的电量为e，质量为m．
18．
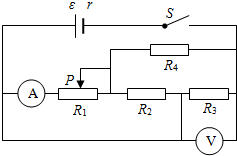如图所示电路中，电源的内电阻为r、R1、R2、R均为定值电阻，电表均为理想电表．闭合开关S，当滑动变阻器R，的滑动触头P向右滑动时，电流表和电压表的示数变化量的大小分别为△I、△U，下列说法正确的是（ ）
如图所示电路中，电源的内电阻为r、R1、R2、R均为定值电阻，电表均为理想电表．闭合开关S，当滑动变阻器R，的滑动触头P向右滑动时，电流表和电压表的示数变化量的大小分别为△I、△U，下列说法正确的是（ ）| A． | 电流表示数变大 | B． | 电压表示数变大 | C． | $\frac{△U}{△I}$＜r | D． | $\frac{△U}{△I}$＞r |
频闪摄影是研究变速运动常用的实验手段．在暗室中，照相机的快门处于常开状态，频闪仪每隔一定时间发出一次短暂的强烈闪光，照亮运动的物体，于是胶片上记录了物体在几个闪光时刻的位置．图中是质量为1.0kg的小球自由下落时的频闪照片（照片中的数字是小球距起点的距离，单位：cm），频闪仪每隔0.04s闪光一次．某同学根据这张频闪照片来《验证机械能守恒定律》，已知当地的重力加速度大小为9.8m/s2，则小球由开始下落到12.5cm过程中小球重力势能减少（填增加或减少）1.23J．小球经过12.5cm处的速度为1.56m/s （以上两空均保留三位有效数字）
15．如图甲所示，abcd是位于竖直平面内的正方形闭合金属线框，在金属线框的下方有一磁感应强度为B的匀强磁场区域，MN和M′N′是匀强磁场区域的水平边界，边界的宽度为S，并与线框的bc边平行，磁场方向与线框平面垂直．现让金属线框由距MN的某一高度从静止开始下落，图乙是金属线框由开始下落到完全穿过匀强磁场区域的v-t图象（其中OA、BC、DE相互平行）．已知金属线框的边长为L（L＜S）、质量为m，电阻为R，当地的重力加速度为g，图象中坐标轴上所标出的字母v1、v2、t1、t2、t3、t4均为已知量．（下落过程中bc边始终水平）根据题中所给条件，以下说法正确的是（ ）
| A． | t2是线框全部进入磁场瞬间，t4是线框全部离开磁场瞬间 | |
| B． | 从bc边进入磁场起一直到ad边离开磁场为止，感应电流所做的功为mgS | |
| C． | V1的大小可能为$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D． | 线框穿出磁场过程中流经线框横截面的电荷量比线框进入磁场过程中流经框横截面的电荷量多 |
14．如图所示，河水流动的速度为v且处处相同，河宽度为a．在船下水点A的下游距离为b处是瀑布．为了使小船渡河安全（不掉到瀑布里去）（ ）
0 142286 142294 142300 142304 142310 142312 142316 142322 142324 142330 142336 142340 142342 142346 142352 142354 142360 142364 142366 142370 142372 142376 142378 142380 142381 142382 142384 142385 142386 142388 142390 142394 142396 142400 142402 142406 142412 142414 142420 142424 142426 142430 142436 142442 142444 142450 142454 142456 142462 142466 142472 142480 176998
| A． | 小船船头垂直河岸渡河时间最短，最短时间为t=$\frac{b}{v}$．速度最大，最大速度为vmax=$\frac{av}{b}$ | |
| B． | 小船轨迹沿y轴方向渡河位移最小．速度最大，最大速度为vmax=$\frac{\sqrt{{a}^{2}+{b}^{2}}v}{b}$ | |
| C． | 小船沿轨迹AB运动位移最大、时间最长．速度最小，最小速度vmin=$\frac{av}{b}$ | |
| D． | 小船沿轨迹AB运动位移最大、速度最小．最小速度vmin=$\frac{av}{\sqrt{{a}^{2}+{b}^{2}}}$ |