题目内容
2.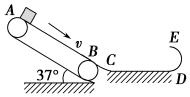 如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面之间通过光滑圆弧BC相连,圆弧BC长度可忽略不计,传送带AB长度为LAB=16m,水平地面长度为LCD=6.3m,半圆轨道DE的半径R=1.125m,物块与水平地面间、传送带间的动摩擦因数均为μ=0.5.求:(sin 37°=0.6,cos 37°=0.8)
如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面之间通过光滑圆弧BC相连,圆弧BC长度可忽略不计,传送带AB长度为LAB=16m,水平地面长度为LCD=6.3m,半圆轨道DE的半径R=1.125m,物块与水平地面间、传送带间的动摩擦因数均为μ=0.5.求:(sin 37°=0.6,cos 37°=0.8)(1)物块在传送带上运动的时间t;
(2)物块到达D点时对D点的压力大小;
(3)物块从E点抛出后的落地点与D点的距离.
分析 (1)根据牛顿第二定律求出物块在传送带上运动的加速度,由速度公式求物块的速度与传送带速度相等时所经历的时间,以及通过的位移,共速后分析物块的受力,再由牛顿第二定律和位移时间公式求出物块运动到B点的时间,从而得到总时间.
(2)物块在CD上做匀减速运动,由牛顿第二定律和速度位移公式求物块到达D点时的速度,再由向心力知识求D点对物块的支持力,从而求得压力.
(2)物块沿半圆轨道从D点运动到E点的过程机械能守恒,由机械能守恒定律求得物块经过E点时的速度,结合平抛运动的规律求出物块从E点抛出后的落地点与D点的距离.
解答 解:(1)刚开始运动时,对物块受力分析,由牛顿第二定律可知:
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=10 m/s2
物块与传送带达到共同速度时有:v=a1t1,
代入数据解得:t1=1 s
物块的位移为:x=$\frac{1}{2}$a1t12=$\frac{1}{2}×10×{1}^{2}$m=5 m
此后对物块受力分析可知:
mgsin 37°-μmgcos 37°=ma2
代入数据解得:a2=2 m/s
物块在传送带上的第二段运动过程有:
LAB-x=vt2+$\frac{1}{2}$a2t22
代入数据解得:t2=1 s
故物块在传送带上运动的总时间为:t=t1+t2=2 s
(2)物块到达传送带底端的末速度为:v2=v+a2t2=10+2×1=12 m/s
在水平地面CD上,物块做匀减速直线运动,其加速度大小为:a=$\frac{μmg}{m}$=μg=5 m/s2
设物块到达D点时的速度为v3,则有:
vD2-v22=-2aLCD
代入数据解得:v3=9 m/s
设此时D点对物块的支持力为FN,根据牛顿第二定律,有:
FN-mg=m$\frac{{v}_{D}^{2}}{R}$
代入数据解得:FN=410 N
根据牛顿第三定律可知,物块对D点的压力大小为410 N.
(3)物块沿半圆轨道从D点运动到E点的过程机械能守恒,设物块经过E点时的速度为vE,根据机械能守恒定律有:
$\frac{1}{2}$mvD2=$\frac{1}{2}$mvE2+2mgR
代入数据解得:vE=6 m/s
物块从E点抛出后做平抛运动,有:
s=vEt3,
2R=$\frac{1}{2}$gt32.
联立并代入数据解得:s=$\frac{9\sqrt{5}}{5}$ m.
答:(1)物块在传送带上运动的时间是2 s;
(2)物块到达D点时对D点的压力大小是410 N;
(3)物块从E点抛出后的落地点与D点的距离是$\frac{9\sqrt{5}}{5}$m.
点评 本题的关键理清物体的运动情况,分段运用牛顿第二定律和运动学公式结合进行研究.要掌握平抛运动的研究方法:运动的分解法.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案| A. | (△v)2($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$) | B. | $\frac{{(△v)}^{2}}{{x}_{2}-{x}_{1}}$ | C. | (△v)2($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$) | D. | 2$\frac{{(△v)}^{2}}{{x}_{2}-{x}_{1}}$ |
 如图所示,在水平转台上放一个质量M的木块,细绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m的小球,当转台以某一恒定角速度转动过程时木块相对转台始终静止,关于木块所受摩擦力说法正确的( )
如图所示,在水平转台上放一个质量M的木块,细绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m的小球,当转台以某一恒定角速度转动过程时木块相对转台始终静止,关于木块所受摩擦力说法正确的( )| A. | 摩擦力大小可能为零 | |
| B. | 若有摩擦力,摩擦力方向可能沿切线方向 | |
| C. | 若有摩擦力,摩擦力方向一定沿半径向外 | |
| D. | 若有摩擦力,摩擦力方向可能指向圆心 |
| A. | 带负电 | B. | 是原来原子的同位素 | ||
| C. | 比原来的原子核多一个质子 | D. | 比原来的原子核多一个中子 |
| A. | 25s | B. | 20s | C. | 15s | D. | 10s |
 如图所示,A是放在地球赤道上的一个物体,正在随地球一起转动.B是赤道上方一颗近地卫星.A和B的质量相等,忽略B的轨道高度,下列说法错误的是( )
如图所示,A是放在地球赤道上的一个物体,正在随地球一起转动.B是赤道上方一颗近地卫星.A和B的质量相等,忽略B的轨道高度,下列说法错误的是( )| A. | A和B做圆周运动的向心加速度大小相等 | |
| B. | A和B受到的地球的万有引力大小相等 | |
| C. | A做圆周运动的线速度比B大 | |
| D. | B做圆周运动的周期比A小 |
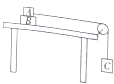 如图,物体A、B的质量分别为mA=10kg,mB=5kg,A与B之间的摩擦因数为μ=0.2,B与水平桌面无摩擦,A物体通过水平细绳跨国定滑轮连接物体C,为保证A、B一起在水平桌面上加速而不发生相对滑动,则物体C的质量mc应满足什么条件?
如图,物体A、B的质量分别为mA=10kg,mB=5kg,A与B之间的摩擦因数为μ=0.2,B与水平桌面无摩擦,A物体通过水平细绳跨国定滑轮连接物体C,为保证A、B一起在水平桌面上加速而不发生相对滑动,则物体C的质量mc应满足什么条件? 如图所示,一质量为m、电荷量为+q的粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°;它运动到B点时速度方向与电场方向的夹角为45°.不计重力.求A、B两点间的电势差为$\frac{m{{v}_{0}}^{2}}{4q}$.
如图所示,一质量为m、电荷量为+q的粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°;它运动到B点时速度方向与电场方向的夹角为45°.不计重力.求A、B两点间的电势差为$\frac{m{{v}_{0}}^{2}}{4q}$.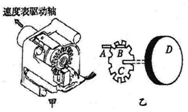 需要测量汽车的速度和行程,图甲为一光电式车速传感器,其原理图乙所示,A为光源,B为光电接受器,A、B均与车身相对固定,旋转齿轮C与车轮D相连接,它们的转速比nC:nD=1:2.车轮转动时A发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号,被B接受并转换成电信号,由电子电路记录和显示.若某次实验显示单位时间内的脉冲数为n,要求出车的速度还必须测量的物理量或数据为测量出车轮的半径R和齿轮数P,汽车速度的表达式为V=$\frac{4πRn}{P}$.
需要测量汽车的速度和行程,图甲为一光电式车速传感器,其原理图乙所示,A为光源,B为光电接受器,A、B均与车身相对固定,旋转齿轮C与车轮D相连接,它们的转速比nC:nD=1:2.车轮转动时A发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号,被B接受并转换成电信号,由电子电路记录和显示.若某次实验显示单位时间内的脉冲数为n,要求出车的速度还必须测量的物理量或数据为测量出车轮的半径R和齿轮数P,汽车速度的表达式为V=$\frac{4πRn}{P}$.