题目内容
14.一质点做匀加速直线运动时,速度变化△v时发生位移x1,紧接着速度变化同样的△v时发生位移x2,则该质点的加速度为( )| A. | (△v)2($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$) | B. | $\frac{{(△v)}^{2}}{{x}_{2}-{x}_{1}}$ | C. | (△v)2($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$) | D. | 2$\frac{{(△v)}^{2}}{{x}_{2}-{x}_{1}}$ |
分析 根据$a=\frac{△v}{△t}$知,发生相同的速度变化所需时间相等,求出时间间隔,根据相邻相等时间位移之差$△x=a{t}_{\;}^{2}$求加速度;
解答 解:发生△v所用的时间为:$t=\frac{△v}{a}$
根据$△x=a{t}_{\;}^{2}$得:${x}_{2}^{\;}-{x}_{1}^{\;}=a•(\frac{△v}{a})_{\;}^{2}$
解得:$a=\frac{(△v)_{\;}^{2}}{{x}_{2}^{\;}-{x}_{1}^{\;}}$,故B正确,ACD错误;
故选:B
点评 本题考查了匀变速直线运动的规律,关键是知道相邻相等时间内位移之差等于$△x=a{t}_{\;}^{2}$

练习册系列答案
相关题目
9.下列各物理量中,属于矢量的是( )
| A. | 力 | B. | 时间 | C. | 质量 | D. | 能量 |
19. 如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
 如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )| A. | $\frac{1}{2}$g | B. | $\frac{2\sqrt{3}}{3}$ g | C. | $\frac{\sqrt{3}}{2}$g | D. | 0 |
6.璧山中学一老师驾车在双星大道正以15m/s的速度匀速行驶,突然他发现前方的红绿灯变为了红灯,于是他立即踩刹车,假设他的车做的是匀减速直线运动,加速度大小为3m/s2,则他踩下刹车后7s内通过的位移为( )
| A. | 37.5 m | B. | 178.5m | C. | 31.5 m | D. | 以上答案都不对 |
3. 在研究影响平行板电容器电容大小的因素的实验中,A、B两板带有等量异种电荷,A板与静电计连接,如图所示,实验中不可能观察到的现象是( )
在研究影响平行板电容器电容大小的因素的实验中,A、B两板带有等量异种电荷,A板与静电计连接,如图所示,实验中不可能观察到的现象是( )
 在研究影响平行板电容器电容大小的因素的实验中,A、B两板带有等量异种电荷,A板与静电计连接,如图所示,实验中不可能观察到的现象是( )
在研究影响平行板电容器电容大小的因素的实验中,A、B两板带有等量异种电荷,A板与静电计连接,如图所示,实验中不可能观察到的现象是( )| A. | 增大A、B板距离,静电计指针张角变大 | |
| B. | 在A、B板间放入厚金属板,静电计指针张角变大 | |
| C. | 把B板向上平移,静电计张角变大 | |
| D. | 在A、B间放入厚玻璃板,静电计指针张角变小 |
 如图所示,传送带与地面的倾角θ=37o,从A到B的长度为16m,传送带以V0=10m/s的速度逆时针转动.在传送带上端无初速的放一个质量为0.5㎏的物体,它与传送带之间的动摩擦因数μ=0.5,(sin37°=0.6,cos37°=0.8)求:
如图所示,传送带与地面的倾角θ=37o,从A到B的长度为16m,传送带以V0=10m/s的速度逆时针转动.在传送带上端无初速的放一个质量为0.5㎏的物体,它与传送带之间的动摩擦因数μ=0.5,(sin37°=0.6,cos37°=0.8)求: 如图所示,质量为50kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑100m到达坡底,用时10s.若g取10m/s2,求:
如图所示,质量为50kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑100m到达坡底,用时10s.若g取10m/s2,求: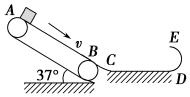 如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面之间通过光滑圆弧BC相连,圆弧BC长度可忽略不计,传送带AB长度为LAB=16m,水平地面长度为LCD=6.3m,半圆轨道DE的半径R=1.125m,物块与水平地面间、传送带间的动摩擦因数均为μ=0.5.求:(sin 37°=0.6,cos 37°=0.8)
如图所示的装置由传送带AB、水平地面CD、光滑半圆形轨道DE三部分组成.一质量为5kg的物块从静止开始沿倾角为37°的传送带上滑下.若传送带顺时针运动,其速度v=10m/s,传送带与水平地面之间通过光滑圆弧BC相连,圆弧BC长度可忽略不计,传送带AB长度为LAB=16m,水平地面长度为LCD=6.3m,半圆轨道DE的半径R=1.125m,物块与水平地面间、传送带间的动摩擦因数均为μ=0.5.求:(sin 37°=0.6,cos 37°=0.8)