题目内容
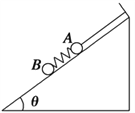
【题目】如图所示，足够长的斜面与水平面的夹角为
，空间中自上而下依次分布着垂直斜面向下的匀强磁场区域Ⅰ、Ⅱ、Ⅲ、……、n，相邻两个磁场的间距均为
．一边长
、质量
、电阻
的正方形导线框放在斜面的顶端，导线框的下边距离磁场Ⅰ的上边界为
，导线框与斜面间的动摩擦因数
.将导线框由静止释放，导线框在每个磁场区域中均做匀速直线运动．已知重力加速度
， 
， 
，求：
（1）导线框进入磁场Ⅰ时的速度；
（2）磁场Ⅰ的磁感应强度
；
（3）磁场区域n的磁感应强度
与
的函数关系．
【答案】(1)2 m/s (2)5 T (3) 
【解析】(1)线框从静止开始运动至刚进入磁场Ⅰ时，以线框为研究对象，由动能定理：
(mgsin θ－μmgcos θ)·d0＝
mv12－0
v1＝2 m/s
(2)线框在磁场Ⅰ中做匀速直线运动，由法拉第电磁感应定律：
E1＝B1Lv1
F1＝B1I1L
mgsin θ－μmgcos θ－F1＝0
B1＝5 T
(3)线框在相邻两个磁场之间加速的距离均为(d－L)＝d0，线框由静止开始运动至刚进入第n个磁场时，由动能定理：n(mgsin θ－μmgcos θ)·d0＝
mvn2－0
又由上可得线框在第一个磁场Ⅰ中受到的安培力
线框在第n个磁场受到的安培力： 
线框在每个磁场区域中均做匀速直线运动，受到的安培力均相等：Fn＝F1
得: 
练习册系列答案
名校课堂系列答案
相关题目
