题目内容
12. 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:(1)a球运动到B点时的速度大小;
(2)a球水平抛出后的落地点E与C点的水平距离.
分析 根据动能定理求出a球运动到B点的速度大小,根据高度求出平抛运动的时间,结合初速度和时间求出水平距离.
解答 解:(1)根据动能定理得,mgh=$\frac{1}{2}m{{v}_{B}}^{2}$,
解得${v}_{B}=\sqrt{2gh}$.
(2)根据$\frac{1}{2}h=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{h}{g}}$,
则水平距离x=${v}_{B}t=\sqrt{2gh}\sqrt{\frac{h}{g}}=\sqrt{2}h$.
答:(1)a球运动到B点时的速度大小为$\sqrt{2gh}$;
(2)a球水平抛出后的落地点E与C点的水平距离为$\sqrt{2}h$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.关于抛体运动,下列说法不正确的是( )
| A. | 做平抛运动的物体运动方向逐渐靠近竖直方向,且速率不断变大,所以是变加速曲线运动 | |
| B. | 平抛运动中物体速度随时间变化是均匀的 | |
| C. | 类平抛运动可分解为初速度方向的匀速直线运动和与之垂直方向上的初速度为零的匀加速直线运动 | |
| D. | 斜抛运动是匀变速曲线运动 |
4.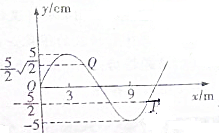 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )| A. | 质点P此时可的振动方向沿y轴负方向 | |
| B. | 质点P的振幅比质点Q的振幅小 | |
| C. | 波的频率为0.25Hz | |
| D. | 质点P,Q的平衡位置间距离为6.5m | |
| E. | 从图示时刻开始,再经$\frac{7}{12}$s,质点P,Q的位移第一次相等 |
1. 如图所示,固定斜面AD上有B、C两点,且AB=BC=CD,小滑块以初动能Ek0从A点出发,沿斜面向上运动,若整个斜面AD光滑,则滑块到达D位置速度恰好为零,而后下滑,现斜面AB部分与滑块间处处有相同的摩擦,其斜部位BD仍无摩擦,则滑块恰好滑到C位置速度为零,然后下滑,那么滑块下滑到( )
如图所示,固定斜面AD上有B、C两点,且AB=BC=CD,小滑块以初动能Ek0从A点出发,沿斜面向上运动,若整个斜面AD光滑,则滑块到达D位置速度恰好为零,而后下滑,现斜面AB部分与滑块间处处有相同的摩擦,其斜部位BD仍无摩擦,则滑块恰好滑到C位置速度为零,然后下滑,那么滑块下滑到( )
 如图所示,固定斜面AD上有B、C两点,且AB=BC=CD,小滑块以初动能Ek0从A点出发,沿斜面向上运动,若整个斜面AD光滑,则滑块到达D位置速度恰好为零,而后下滑,现斜面AB部分与滑块间处处有相同的摩擦,其斜部位BD仍无摩擦,则滑块恰好滑到C位置速度为零,然后下滑,那么滑块下滑到( )
如图所示,固定斜面AD上有B、C两点,且AB=BC=CD,小滑块以初动能Ek0从A点出发,沿斜面向上运动,若整个斜面AD光滑,则滑块到达D位置速度恰好为零,而后下滑,现斜面AB部分与滑块间处处有相同的摩擦,其斜部位BD仍无摩擦,则滑块恰好滑到C位置速度为零,然后下滑,那么滑块下滑到( )| A. | 位置B时的动能为$\frac{{E}_{{k}_{0}}}{3}$ | B. | 位置B时的动能为$\frac{{E}_{{k}_{0}}}{2}$ | ||
| C. | 位置A时的动能为$\frac{{E}_{{k}_{0}}}{2}$ | D. | 位置A时的动能为$\frac{{E}_{{k}_{0}}}{3}$ |
 如图所示,质量为2kg的物体A静止在竖直的轻弹簧上面,若将一个质量为3kg的物体B轻轻放在A上,刚刚放上瞬间,B对A的压力大小为(取g=10m/s2)( )
如图所示,质量为2kg的物体A静止在竖直的轻弹簧上面,若将一个质量为3kg的物体B轻轻放在A上,刚刚放上瞬间,B对A的压力大小为(取g=10m/s2)( )
 如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?
如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?