题目内容
4.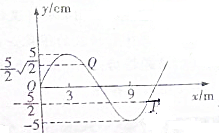 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )| A. | 质点P此时可的振动方向沿y轴负方向 | |
| B. | 质点P的振幅比质点Q的振幅小 | |
| C. | 波的频率为0.25Hz | |
| D. | 质点P,Q的平衡位置间距离为6.5m | |
| E. | 从图示时刻开始,再经$\frac{7}{12}$s,质点P,Q的位移第一次相等 |
分析 根据简谐波的特点:各个质点的振幅都相同,分析PQ的振幅关系.根据此时P点的位置和状态,写出质点P的振动方程.
解答 解:
A、简谐横波沿x轴正方向传播,波形向右平移,则知质点P此时刻的振动方向沿y轴负方向.故A正确;
B、该波是简谐横波,所以P点与Q点的振幅相等,故B错误;
C、由图知波长λ=12m,则周期 T=$\frac{λ}{v}$=$\frac{12}{3}$s=4s,频率:$f=\frac{1}{T}=\frac{1}{4}=0.25$Hz,故C正确;
D、由图可知,该波的振幅为5cm,角频率:$ω=\frac{2π}{T}=\frac{2π}{4}=0.5π$rad/s.则该波的波动方程为:y=0.05sin(ωt-$\frac{x}{v}$),在t=0时刻,P点的位移是$\frac{5\sqrt{2}}{2}$cm,Q点的位移是:$-\frac{5\sqrt{2}}{2}$cm,将各数据代入,得:xP=4.5,xQ=10.5m.所以质点P,Q的平衡位置间距离为6.0m.故D错误;
E、由于质点P,Q的平衡位置间距离为6.0m,等于半个波长,所以质点P,Q的位移第一次相等时一定都在平衡位置,满足:$t=\frac{{x}_{Q}}{v}=\frac{4.5}{3}=1.5$s,故E错误.
故选:AC.
点评 解决本题要抓住波的基本特点:各个质点的振幅都相同,要能根据质点的初始位置确定初相位,再写出振动方程即可正确解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )
如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )
 如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )
如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )| A. | 16mg | B. | 22mg | C. | 28mg | D. | 0 |
9. 如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
 如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )| A. | 甲、乙、丙在空中的运动时间之比等于1:2:2 | |
| B. | 甲、乙、丙初速度之比等于1:$\sqrt{2}$:2$\sqrt{2}$ | |
| C. | 落地前甲、乙、丙的速度方向相同 | |
| D. | 空中运动过程中甲、乙、丙增加的动能之比等于1:4:6 |
16.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,速度大小减小为原来的$\frac{1}{2}$,则变轨前后卫星的( )
| A. | 轨道半径之比为1:2 | B. | 向心加速度大小之比为4:1 | ||
| C. | 角速度大小之比为2:1 | D. | 周期之比为1:8 |
13.万有引力定律的表达式是F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | r是两物体之间最近的距离 | |
| B. | 当r=0时,万有引力无穷大 | |
| C. | 引力常量G是人为规定的 | |
| D. | 两物体受到的万有引力总是大小相等,与两物体质量是否相等无关 |
 光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求:
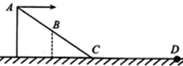
光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求: 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求: 如图所示,两完全相同的金属棒垂直放在水平光滑导轨上,其质量均为m=1kg,导轨间距d=0.5m,现两棒并齐,中间夹一长度不计的轻质压缩弹簧,弹簧弹性势能为Ep=16J.现释放弹簧(与两棒不拴接),两金属棒获得大小相等的速度,且ab棒平行导轨进入一随时间变化的磁场,已知B=2+0.5t(单位:T),方向垂直导轨平面向下,导轨上另有两个挡块P、Q,cd棒与之碰撞时无能量损失,Pc=aM=16m,两棒电阻均为R=5Ω,导轨电阻不计,若从释放弹簧时开始计时(不考虑弹簧弹开两棒的时间),在ab棒进入磁场边界的瞬间,加一外力F(大小和方向都可以变化),使之始终做加速度a=0.5m/s2的匀减速直线运动,求:
如图所示,两完全相同的金属棒垂直放在水平光滑导轨上,其质量均为m=1kg,导轨间距d=0.5m,现两棒并齐,中间夹一长度不计的轻质压缩弹簧,弹簧弹性势能为Ep=16J.现释放弹簧(与两棒不拴接),两金属棒获得大小相等的速度,且ab棒平行导轨进入一随时间变化的磁场,已知B=2+0.5t(单位:T),方向垂直导轨平面向下,导轨上另有两个挡块P、Q,cd棒与之碰撞时无能量损失,Pc=aM=16m,两棒电阻均为R=5Ω,导轨电阻不计,若从释放弹簧时开始计时(不考虑弹簧弹开两棒的时间),在ab棒进入磁场边界的瞬间,加一外力F(大小和方向都可以变化),使之始终做加速度a=0.5m/s2的匀减速直线运动,求: