题目内容
17.在Oxy平面内的OPMN区域内,存在两个场强大小均为E、方向分别水平向左和竖直向上E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形,两电场之间存在一段宽为L的真空区域,已知电子的质量为m,电子的电量大小为e,不计电子所受重力.求: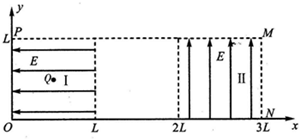
(1)在该区域OP边的中点处由静止释放电子,电子进入Ⅱ区域时速度的大小;
(2)若在Ⅰ区域内坐标为($\frac{L}{2}$,$\frac{L}{2}$)的Q点由静止释放电子,则电子离开Ⅱ区域时的速度的大小.
分析 (1)电子在电场I区域做初速度为0的匀加速运动,根据动能定理求速度(2)根根据电子在电场I中做匀加速运动,在两电场间做匀速直线运动,进入电场II做类平抛运动,离开电场II做匀速直线运动,根据运动的合成与分解求解电子离开OABC区域的位置坐标,求速度.
解答 解:(1)电子在电场I区域做初速度为0的匀加速直线运动,根据动能定理有电子离开电场I时的速度:
eEL=$\frac{1}{2}$mv2
可得电子速度为:v=$\sqrt{\frac{2eEl}{m}}$
(2)电子离开电场I后做匀速直线运动后再进入电场II,在电场II中电子具有水平方向的初速度和竖直方向的电场力,电子做类平抛运动,由动能定理得:水平方方向为:v=$\sqrt{\frac{eEl}{m}}$
水平方方向做匀速直线运动满足:L=vt…①
在竖直方向做初速度为0的匀加速直线运动:y=$\frac{1}{2}$at2…②
在竖直方向上的加速度为:a=$\frac{eE}{m}$…③
由①②③可解得电子在电场II区域内偏转的位移为:y=$\frac{l}{2}$
电子离开电场II的速度大小为:
eE$\frac{l}{2}$=$\frac{1}{2}$mv′2-$\frac{1}{2}$mv2
解得:v′=$\sqrt{\frac{2eEl}{m}}$
答:(1)电子进入Ⅱ区域时速度的大小$\sqrt{\frac{2eEl}{m}}$
(2)电子离开Ⅱ区域时的速度的大小$\sqrt{\frac{2eEl}{m}}$.
点评 分析电子在电场中的受力特点,根据运动特征确定电子的运动情况,再根据运动的规律求解.掌握运动的合成与分解求解曲线运动的规律是正确解题的关键

练习册系列答案
相关题目
7. 如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
 如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )
如图所示,质量为m的物体以速度v0离开桌面后经过A点时,所具有的机械能是(以桌面为零势能面,不计空气阻力)( )| A. | $\frac{1}{2}$mv02 | B. | $\frac{1}{2}$mv02+mgh | C. | $\frac{1}{2}$mv02-mgh | D. | $\frac{1}{2}$mv02+mg(H-h) |
8. 在如图所示的齿轮传动中,三个齿轮的半径之比为2:3:6,当齿轮转动的时候,小齿轮边缘的A点和大齿轮边缘的B点满足( )
在如图所示的齿轮传动中,三个齿轮的半径之比为2:3:6,当齿轮转动的时候,小齿轮边缘的A点和大齿轮边缘的B点满足( )
 在如图所示的齿轮传动中,三个齿轮的半径之比为2:3:6,当齿轮转动的时候,小齿轮边缘的A点和大齿轮边缘的B点满足( )
在如图所示的齿轮传动中,三个齿轮的半径之比为2:3:6,当齿轮转动的时候,小齿轮边缘的A点和大齿轮边缘的B点满足( )| A. | A点和B点的线速度大小之比是1:1 | B. | A点和B点的角速度之比为1:1 | ||
| C. | A点和B点的周期之比为1:3 | D. | A点和B点的向心加速度之比为1:3 |
5.下列关于力的说法,正确的是( )
| A. | 两个物体一接触就会产生弹力 | |
| B. | 物体的重心不一定在物体上 | |
| C. | 滑动摩擦力的方向和物体运动方向相反 | |
| D. | 合力的大小可以小于任何一个分力的大小 |
9.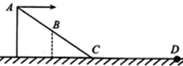 如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
 如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )
如图所示,将甲、乙、丙三个小球从固定斜面的顶端A水平抛出,它们的质量之比分别为1:2:3,分别落在斜面的中点B,底端C和水平面上的D点,已知CD的距离等于AC间的水平距离,不计空气阻力,则下列说法正确的是( )| A. | 甲、乙、丙在空中的运动时间之比等于1:2:2 | |
| B. | 甲、乙、丙初速度之比等于1:$\sqrt{2}$:2$\sqrt{2}$ | |
| C. | 落地前甲、乙、丙的速度方向相同 | |
| D. | 空中运动过程中甲、乙、丙增加的动能之比等于1:4:6 |
 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求: 如图所示,水平光滑地面上停放着一辆质量3m的小车,左侧靠在竖直墙壁上,小车上的AB部分为半径为R的$\frac{1}{4}$圆弧光滑轨道,轨道的最低点B与水平粗糙轨道BC相切,整个轨道处于同一竖直平面内.质量m的物块(可视为质点)从A点正上方距A点竖直高度3R处静止下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行.已知物块与水平轨道BC间的动摩擦因素μ=0.3,重力加速度g,不考虑空气阻力和物块落入圆弧轨道时的机械能损失.求:
如图所示,水平光滑地面上停放着一辆质量3m的小车,左侧靠在竖直墙壁上,小车上的AB部分为半径为R的$\frac{1}{4}$圆弧光滑轨道,轨道的最低点B与水平粗糙轨道BC相切,整个轨道处于同一竖直平面内.质量m的物块(可视为质点)从A点正上方距A点竖直高度3R处静止下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行.已知物块与水平轨道BC间的动摩擦因素μ=0.3,重力加速度g,不考虑空气阻力和物块落入圆弧轨道时的机械能损失.求:
 在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.某同学在做实验时,只记录了小球在运动过程中的A、B、C三点的位置,取A点为坐标原点,建立直角坐标系(y轴为铅直方向),各点的坐标如图所示.g取10m/s2.则小球抛出点的坐标是(-20,-5);小球经过B点时的速度大小是2$\sqrt{2}$m/s.(结果可以用根式表示)
在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.某同学在做实验时,只记录了小球在运动过程中的A、B、C三点的位置,取A点为坐标原点,建立直角坐标系(y轴为铅直方向),各点的坐标如图所示.g取10m/s2.则小球抛出点的坐标是(-20,-5);小球经过B点时的速度大小是2$\sqrt{2}$m/s.(结果可以用根式表示)