题目内容
2.如图1所示,将打点计时器固定在铁架台上,使重物带动纸带从静止开始自由下落,利用此装置可以验证机械能守恒定律.(1)小张所在的实验小组利用该实验装置验证机械能守恒定律,已知实验所用重物的质量为m,打点计时器打点周期为T,当地重力加速度为g.如图2所示为实验得到的一条点迹清晰的纸带,把第一个点记做O,另选连续的3个点A、B、C作为测量点.经测量A、B、C各点到O点的距离分别为S1、S2、S3.根据以上测量结果可知当打点计时器打下B点时重物重力势能减少量△Ep=mgS2,动能增加量等于△Ek=$\frac{{m({{S}_{3}-S}_{1})}^{2}}{{8T}^{2}}$.(用m、T、g、S1、S2、S3表示)

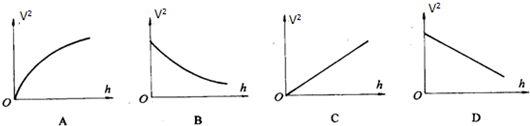
(2)小黄所在的实验小组也用该实验装置,采用作图法来验证机械能守恒定律,如果以v2为纵轴,以h(h为各点到初始点O的距离)为横轴,如图ABCD选项中是四个同学根据实验数据绘出的v2-h图线,则正确的图象是:C,根据正确的v2-h图线,该图线的斜率等于2g.
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.根据机械能守恒定律得出v2-h的关系式,从而确定正确的图线;
解答 解:(1)利用匀变速直线运动的推论得:
vB=$\frac{{{S}_{3}-S}_{1}}{2T}$
重物重力势能减少量△Ep=mgh=mgS2
动能增加量等于△Ek=$\frac{1}{2}$m${v}_{B}^{2}$-0=$\frac{{m({{S}_{3}-S}_{1})}^{2}}{{8T}^{2}}$,
(2)重物由静止开始下落距离h获得速度v,根据动能定理得
mgh=$\frac{1}{2}$mv2
即v2=2gh
所以v2-h图线是过原点的倾斜直线(或正比例函数图象等),
故选:C
该图线的斜率是 2g.
故答案为:(1)mgS2 ;$\frac{{m({{S}_{3}-S}_{1})}^{2}}{{8T}^{2}}$
(2)C;2g
点评 运用运动学公式和动能、重力势能的定义式解决问题是该实验的常规问题,同时要熟练应用基本物理规律解决实验问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.万有引力定律的表达式是F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | r是两物体之间最近的距离 | |
| B. | 当r=0时,万有引力无穷大 | |
| C. | 引力常量G是人为规定的 | |
| D. | 两物体受到的万有引力总是大小相等,与两物体质量是否相等无关 |
8.如图所示,在匀速转动的圆筒内壁上紧靠着一个物体一起运动,充当物体所受向心力的是( )


| A. | 重力 | B. | 静摩擦力 | C. | 弹力 | D. | 滑动摩擦力 |
9.下列说法正确的是( )
| A. | 当分子间作用力表现为斥力时,分子势能随分子间距离的增大而增大 | |
| B. | 温度高的物体分子平均动能一定大,内能也一定大 | |
| C. | 昆虫可以停在水面上,主要是液体表面张力的作用 | |
| D. | 热力学第二定律指出:在任何自然的过程中,一个孤立的系统的总熵不会减小 |
 如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求:
如图所示,a球从距BC高h的A处静止释放后,沿光滑轨道ABC下滑,在C处水平抛出.已知C离水平地面的高度为$\frac{1}{2}$h,重力加速度为g,求: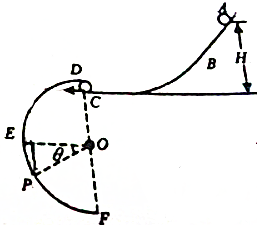 如图所示,ABC和DEF是在同一竖直平面内的两条光滑的轨道,其中ABC的末端水平,DEF是半径为r的半圆形轨道,其直径DF沿竖直方向,C、D间距很小,现有一可视为质点的小球从轨道ABC上距点高为H的地方由静止释放.
如图所示,ABC和DEF是在同一竖直平面内的两条光滑的轨道,其中ABC的末端水平,DEF是半径为r的半圆形轨道,其直径DF沿竖直方向,C、D间距很小,现有一可视为质点的小球从轨道ABC上距点高为H的地方由静止释放. 在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.某同学在做实验时,只记录了小球在运动过程中的A、B、C三点的位置,取A点为坐标原点,建立直角坐标系(y轴为铅直方向),各点的坐标如图所示.g取10m/s2.则小球抛出点的坐标是(-20,-5);小球经过B点时的速度大小是2$\sqrt{2}$m/s.(结果可以用根式表示)
在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线方向保持水平;实验时,每次使小球由静止滚下都应注意从同一高度.某同学在做实验时,只记录了小球在运动过程中的A、B、C三点的位置,取A点为坐标原点,建立直角坐标系(y轴为铅直方向),各点的坐标如图所示.g取10m/s2.则小球抛出点的坐标是(-20,-5);小球经过B点时的速度大小是2$\sqrt{2}$m/s.(结果可以用根式表示) 如图所示,两完全相同的金属棒垂直放在水平光滑导轨上,其质量均为m=1kg,导轨间距d=0.5m,现两棒并齐,中间夹一长度不计的轻质压缩弹簧,弹簧弹性势能为Ep=16J.现释放弹簧(与两棒不拴接),两金属棒获得大小相等的速度,且ab棒平行导轨进入一随时间变化的磁场,已知B=2+0.5t(单位:T),方向垂直导轨平面向下,导轨上另有两个挡块P、Q,cd棒与之碰撞时无能量损失,Pc=aM=16m,两棒电阻均为R=5Ω,导轨电阻不计,若从释放弹簧时开始计时(不考虑弹簧弹开两棒的时间),在ab棒进入磁场边界的瞬间,加一外力F(大小和方向都可以变化),使之始终做加速度a=0.5m/s2的匀减速直线运动,求:
如图所示,两完全相同的金属棒垂直放在水平光滑导轨上,其质量均为m=1kg,导轨间距d=0.5m,现两棒并齐,中间夹一长度不计的轻质压缩弹簧,弹簧弹性势能为Ep=16J.现释放弹簧(与两棒不拴接),两金属棒获得大小相等的速度,且ab棒平行导轨进入一随时间变化的磁场,已知B=2+0.5t(单位:T),方向垂直导轨平面向下,导轨上另有两个挡块P、Q,cd棒与之碰撞时无能量损失,Pc=aM=16m,两棒电阻均为R=5Ω,导轨电阻不计,若从释放弹簧时开始计时(不考虑弹簧弹开两棒的时间),在ab棒进入磁场边界的瞬间,加一外力F(大小和方向都可以变化),使之始终做加速度a=0.5m/s2的匀减速直线运动,求: