Question

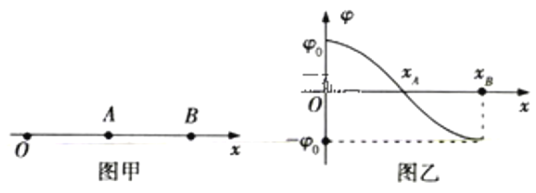
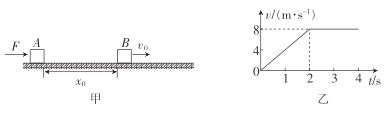
【题目】如图甲所示，在足够大的水平地面上有A、B两物块(均可视为质点)。t=0时刻，A、B的距离x0=6m，A在水平向右的推力F作用下，其速度—时间图象如图乙所示。t=0时刻，B的初速度大小v0=12m/s、方向水平向右，经过一段时间后两物块发生弹性正碰。已知B的质量为A的质量的3倍，A、B与地面间的动摩擦因数分别为μ1=0.1、=0.4，取g=10m/s2。

(1)求A、B碰撞前B在地面上滑动的时间t1以及距离x1；

(2)求从t=0时刻起到A与B相遇的时间t2；

(3)若在A、B碰撞前瞬间撤去力F，求A、B均静止时它们之间的距离x。

Answer 1

【答案】(1)3s，18m(2)4s(3)10m

【解析】

(1)设B的质量为3m，A、B碰撞前B在地面上滑动的加速度大小为a，根据牛顿第二定律有

若A、B碰撞前B已停止运动，则由匀变速直线运动的规律有：

解得

=3s，=18m

由题图乙可得，0~3s时间内A滑动的距离为：

m=16m

由于

=24m

故A、B碰撞前B已停止运动，假设成立。

(2)由(1)可知=3s时，A、B尚未发生碰撞，故A、B碰撞前瞬间A的速度大小为：

=8m/s

经分析可知

解得：

=4s

(3)设碰撞后瞬间A、B的速度分别为、，有：

解得：

=4m/s(为负值，说明的方向水平向左)，=4m/s

设A、B碰撞后滑行的距离分別为L1、L2，有：，

根据动能定理有：

解得：

x=10m