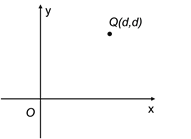
题目内容
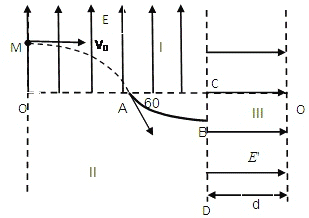
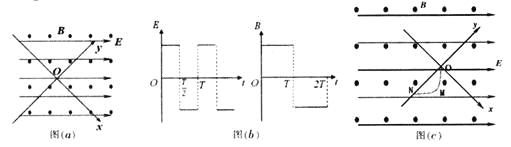
【题目】如图(a)所示,在竖直平面内建立直角坐标系xoy,整个空间内都存在垂直于坐标平面向外的匀强磁场和水平向右的匀强电场,匀强电场的方向与x轴止方向夹角为450。已知带电粒子质量为m、电量为+q,磁感应强度大小为B,电场强度大小E![]() ,重力加速度为g.
,重力加速度为g.
(1)若粒子在xoy平面内做匀速直线运动,求粒子的速度v0;
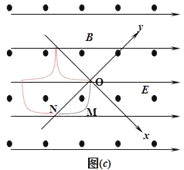
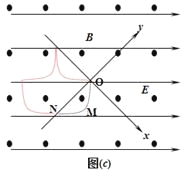
(2)t=0时刻的电场和磁场方向如图(a)所示,若电场强度和磁感应强度的大小均不变.而方向随时间周期性的改变,如图(b)所示。将该粒子从原点O由静止释放,在0一![]() 时间内的运动轨迹如图(c)虚线OMN所示,M点为轨迹距y轴的最远点,M距y轴的距离为d。已知在曲线上某一点能找到一个和它内切的半径最大的圆,物休经过此点时,相当于以此圆的半径在做圆周运动,这个圆的半径就定义为曲线上这点的曲率半径。求:
时间内的运动轨迹如图(c)虚线OMN所示,M点为轨迹距y轴的最远点,M距y轴的距离为d。已知在曲线上某一点能找到一个和它内切的半径最大的圆,物休经过此点时,相当于以此圆的半径在做圆周运动,这个圆的半径就定义为曲线上这点的曲率半径。求:
①粒子经过M点时曲率半径![]()
②在图中画出粒子从N点回到O点的轨迹。
【答案】(1)![]() ,沿y轴负方向(2)
,沿y轴负方向(2)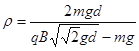 ,
,
如图所示
【解析】试题分析:(1)粒子做匀速直线运动,受力平衡得
![]()
解得![]()
v0方向由左手定则得,沿y轴负方向。
(2)①解法(一)
重力和电场力的合力为![]()
粒子从O运动到M过程中,只有重力和电场力的合力做功,据动能定理
![]() (若分别求出重力功、电场力功各1分)
(若分别求出重力功、电场力功各1分)
得 v=![]()
由![]()
得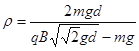 (若用
(若用![]() 代入,求出
代入,求出![]() 也给分)
也给分)
解法(二)
粒子的运动可看作以速度![]() 沿y轴负方向的匀速直线运动和以
沿y轴负方向的匀速直线运动和以![]() 沿顺时针方向的匀速圆周运动的合运动, 其中沿y轴负方向的
沿顺时针方向的匀速圆周运动的合运动, 其中沿y轴负方向的![]() 对应的洛仑兹力用来与等效重力平衡,即
对应的洛仑兹力用来与等效重力平衡,即
![]() ,
,
沿y轴正方向的![]() 对应的洛仑兹力用来提供向心力,即
对应的洛仑兹力用来提供向心力,即![]()
到达M点时,其两分速度同向,沿x轴正方向的位移为d,则有![]()
![]()
由洛仑兹力和等效重力的合力提供向心力,![]()
得M点的曲率半径![]()
②轨迹如图所示。(画对第一段2分,画对前二段4分,全部画对得6分)

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目