题目内容
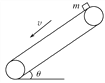
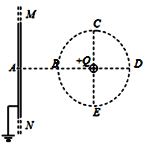
【题目】如图所示,区域Ⅰ内有电场强度为E=2×104N/C、方向竖直向上的匀强电场;区域Ⅱ中有一光滑绝缘圆弧轨道,轨道半径为R= 2m,轨道在A点的切线与水平方向成60°角,在B点的切线与竖直线CD垂直;在Ⅲ区域有一宽为d=3m的有界匀强电场,电场强度大小未知,方向水平向右.一质量为m=0.4kg、带电荷量为q= -2×10-4C的小球(质点)从左边界O点正上方的M点以速度v0=2m/s水平射入区域 I,恰好从A点沿圆弧轨道切线进入轨道且恰好不能从Ⅲ区域中电场的右边界穿出,(取g=10m/S2)求:
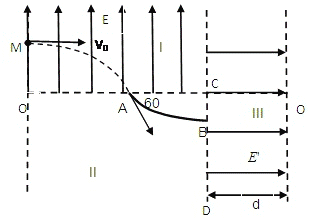
(1)OM的长L;
(2)区域Ⅲ中电场的电场强度大小E′;
(3)小球到达区域Ⅲ中的电场边界上的点与oo′的距离.
【答案】(1) 0.3m (2) 1.2×104N/C (3) ![]()
【解析】(1)小球在区域 I中做类平抛运动,设小球在A点的速度为vA,竖直分速度为vy,
则有: ![]() ,
, ![]()
由牛顿第二定律可得: ![]()
由匀变速直线运动的速度位移公式得: ![]() ,解得:
,解得: ![]() ;
;
(2)在区域 II中,由图可能得,由A至B下降的高度为![]() ,
,
则由A到B,根据动能定理:mg![]() =
=![]() mvB2 —
mvB2 —![]() mvA2,解得:vB=3v0
mvA2,解得:vB=3v0
在区域 III中,小球在水平方向做匀减速直线运动,到达右边界时水平速度刚好减为零,
由匀变速直线运动的速度位移公式得:vB2=2![]() d
d
解得:E′=1.2×104N/C;
(3)水平方向: ![]() ,
, ![]()
代入数据得: ![]()
坚直方向上小球做自由落体运动: ![]()
小球到达右边界后又向左返回到左边界,返回用时![]()
竖直方向下落的高度 ![]()
所以小球到达区域Ⅲ中电场边界上时与![]() 的距离为:
的距离为:
![]() ,
, ![]() ,即:
,即: ![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目