题目内容
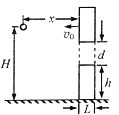
【题目】在竖直平面内有与平面平行的匀强电场，一质量为m、带电量为+q的小球从竖直平面的坐标原点O处以某一速度抛出，已知小球经y轴上的某点P点时速度最小，小球经Q点时速度大小与O点的速度大小相同，且xQ=d，yQ=d，如图所示。已知重力加速度为g，求：
（1）电场强度的最小值
（2）若电场强度为(1)中所求的值，则
①小球从O点抛出时的初速度的大小
②小球再次经过x轴的坐标。
【答案】（1）
q，方向沿OQ方向 （2）①
②3d
【解析】试题分析：由于小球在O、Q两点的速度大小相等，则小球所受重力和电场力的合力F的方向应与OQ垂直，根据平衡条件可得电场强度的最小值；当E取最小值时，合力
，小球运动过程中的加速度为
方向与y轴负方向成450角，由于小球在P点速度最小，根据运动学公式即可求得小球从O点抛出时的初速度的大小；画出轨迹根据平抛运动公式和几何关系即可求出小球再次经过x轴的坐标。
（1）由于小球在O、Q两点的速度大小相等，则小球所受重力和电场力的合力F的方向应与OQ垂直，又OQ与x轴的夹角tanθ=1，即θ=450，所以合力与y轴负方向的夹角为θ，如图所示：
有qE=mgcos450，
解得： 
，方向沿OQ方向
(2) ①当E取最小值时，合力
，小球运动过程中的加速度为
方向与y轴负方向成450角，由于小球在P点速度最小，则P点O、Q两点对称，易得P点坐标为(0,d)。在P点，小球速度方向应沿OQ方向，设P点的速度为v，
易得： 
解得： 
，
在O点的速度v0应有： 
解得： 
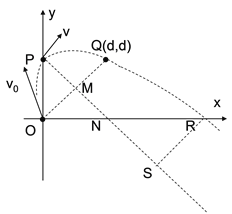
②设小球运动轨迹与x轴交点为R，小球从P到R做类平抛运动，设PMS交x轴为N，RS与PS垂直，
有
位移关系为： 
根据几何关系有： 
解得： 
所以： 
练习册系列答案
相关题目
