题目内容
【题目】如图所示，有理想边界的两个匀强磁场，磁感应强度B=0.5T，两边界间距s=0.1m．一边长L=0.2m的正方形线框abcd由粗细均匀的电阻丝围成，总电阻R=0.4Ω。现使线框以v=2m/s的速度从位置I匀速运动到位置Ⅱ。
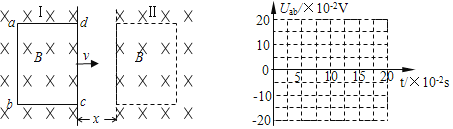
(1)求cd边未进入右方磁场时线框所受安培力的大小．
(2)求整个过程中线框所产生的焦耳热．
(2)在坐标图中画出整个过程中线框a、b两点的电势差Uab随时间t变化的图线．
【答案】(1)5x10-2N；(2)0.01J；(3)如图：
【解析】
（1）cd边未进入右方磁场时线框时，ab边切割产生感应电动势，大小为:
E=BLv=0.5×0.2×2V=0.2V
由闭合电路欧姆定律得感应电流大小为：
ab边受到的安培力大小为F安=BIL=0.5×0.05×2N=0.05N
（2）设克服安培力做得功为W安，由功能关系得：整个过程中线框所产生的焦耳热
Q=2W安=2F安s=2×0.05×0.1J=0.01J
（3）cd边未进入磁场，ab两端电势差Uab＝
E＝0.15V，由楞次定律判断出感应电流方向沿顺时针方向，则a的电势高于b的电势，Uab为正。
cd边进入磁场后，线框中虽然感应电流为零，但ab两端仍有电势差，由右手定则判断可知，a的电势高于b的电势，Uab为正，所以Uab=E=0.20V
ab边穿出磁场后，只有cd边切割磁感线，由右手定则知，a点的电势高于b的电势，Uab＝
E＝0.05V．
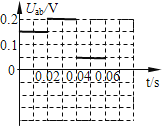
整个过程中线框a、b两点的电势差Uab随时间t变化的图线如下图所示：
练习册系列答案
阅读快车系列答案
相关题目
