题目内容
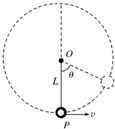如图所示，长为L的轻绳一端固定在O点，另一端系一小球（可视为质点），小球在竖直平面内沿逆时针方向做圆周运动．已知小球运动过程中轻绳拉力大小FT和竖直方向OP的夹角θ的关系为：FT=b+bcosθ，b为已知的常数，当地重力加速度为g，不计空气阻力，求小球的质量．分析：分别求出当θ=0°和180°时绳子的拉力，再根据向心力公式及动能定理列式即可求解．
解答：解：设小球在圆周的最低点即θ=0°时速度为v1，此时轻绳上拉力FT=2b
由牛顿第二定律得2b-mg=m
小球在圆周的最高点即θ=180°时速度为v2，此时轻绳上拉力FT=0
由牛顿第二定律得mg=m
从最低点到最高点，由机械能守恒得：
mv
=
mv
+2mgL
由以上几式解得m=
．
答：小球的质量为
．
由牛顿第二定律得2b-mg=m
| v12 |
| L |
小球在圆周的最高点即θ=180°时速度为v2，此时轻绳上拉力FT=0
由牛顿第二定律得mg=m
| v12 |
| L |
从最低点到最高点，由机械能守恒得：
| 1 |
| 2 |
2 1 |
| 1 |
| 2 |
2 2 |
由以上几式解得m=
| b |
| 3g |
答：小球的质量为
| b |
| 3g |
点评：本题主要考查了向心力公式及动能定理的应用，要求同学们能找出向心力的来源，难度适中．
练习册系列答案
相关题目
（2004?天津模拟）如图所示，长为l的轻杆一端固定一质量为m的小球，另一端有固定转轴O，杆可在竖直平面内绕转轴O无摩擦转动．已知小球通过最低点Q时，速度大小为v=2
如图所示，长为L的轻杆一端固定一个小球，另一端固定在光滑水平轴上，使小球在竖直平面内做圆周运动，设小球在过最高点A点的速度v，下列叙述中正确的是（ ）
如图所示，长为L的轻绳一端固定于O点，另一端系一个小球．现使小球在竖直平面内做圆周运动，P是圆周轨道最高点，Q是轨道最低点．已知重力加速度为g．若小球刚好能够通过最高点P，则以下判断正确的是（ ）
如图所示，长为L的轻杆两端各连一个质量均为m的小球（半径可以忽略不计），以它们的中点为轴，在竖直平面内做匀速圆周运动，转动周期为T=2π
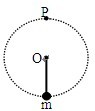如图所示，长为L的轻杆一端固定质量为m的小球，另一端有固定转轴O，现使小球在竖直平面内做圆周运动，P为圆周的最高点，若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点，且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点，且在P点受到轻杆向上的支持力 |