题目内容
 (2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2
(2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2| gl |
分析:先根据动能定理判断小球能否到达P点,若能则小球在最高点时竖直方向上的合力提供向心力,根据牛顿第二定律,求出小球在最高点的合力,从而确定小球受到的是拉力还是支持力.
解答:解:根据动能定理得,-mg?2l=
mv′2-
mv2
解得v′=0.知小球能够到达最高点P.此时在最高点重力和支持力相等,即在P点收到轻杆对它向上的弹力.故C正确,A、B、D错误.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
解得v′=0.知小球能够到达最高点P.此时在最高点重力和支持力相等,即在P点收到轻杆对它向上的弹力.故C正确,A、B、D错误.
故选C.
点评:解决本题的关键知道圆周运动径向的合力提供向心力,以及知道杆子的作用力可以表现为支持力,也可以表现为拉力.

练习册系列答案
相关题目
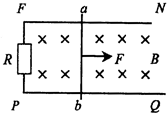 (2004?天津模拟)如图所示,平行金属导轨MN、PQ水平放置,接电阻为R的固定电阻.金属棒ab垂直于导轨放置,且始终与导轨接触良好.导轨和金属棒的电阻不计.匀强磁场方向垂直导轨所在平面.现用垂直于ab棒的水平向右的外力F,拉动ab棒由静止开始向右做匀加速直线运动.则图中哪一个能够正确表示外力F随时间变化的规律?( )
(2004?天津模拟)如图所示,平行金属导轨MN、PQ水平放置,接电阻为R的固定电阻.金属棒ab垂直于导轨放置,且始终与导轨接触良好.导轨和金属棒的电阻不计.匀强磁场方向垂直导轨所在平面.现用垂直于ab棒的水平向右的外力F,拉动ab棒由静止开始向右做匀加速直线运动.则图中哪一个能够正确表示外力F随时间变化的规律?( ) (2004?天津模拟)如图画出了匀强电场的几条电场线,M、N是该电场中的两点.一个带正电荷的离子(不计重力)仅在电场力作用下由M点运动到N点,则( )
(2004?天津模拟)如图画出了匀强电场的几条电场线,M、N是该电场中的两点.一个带正电荷的离子(不计重力)仅在电场力作用下由M点运动到N点,则( )