��Ŀ����
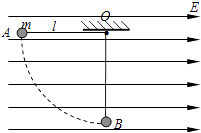
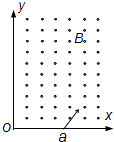
����Ŀ����ͼ��ʾ��һ����m=0.4kg�Ļ��飨����Ϊ�ʵ㣩��ֹ�ڶ�Ħ��������=0.1��ˮƽ����ϵ�A�㣮�ֶԻ���ʩ��һˮƽ������ʹ�������˶��������Ĺ��ʺ�ΪP=10.0W������һ��ʱ���ȥ�������������������B���ˮƽ�ɳ���ǡ����C�������߷������̶�����ֱƽ���ڵĹ⻬Բ���ι�����������͵�D��װ��ѹ���������������鵽�ﴫ�����Ϸ�ʱ����������ʾ��Ϊ25.6N����֪���AB�ij���L=2.0m���뾶OC����ֱ����ļнǦ�=37�㣬Բ�ι���İ뾶R=0.5m�������������ɺ��ԣ��������ٶ�g=10m/s2 �� sin37��=0.6��cos37��=0.8��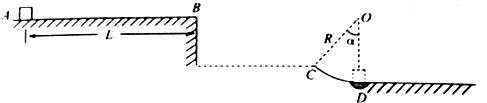
��
��1�������˶���C��ʱ�ٶ�vc�Ĵ�С��
��2��B��C����ĸ߶Ȳ�h��ˮƽ����x��
��3��ˮƽ���������ڻ����ϵ�ʱ��t��
���𰸡�
��1���⣺�����˶���D��ʱ����ţ�ٵڶ����ɵã�
![]() ��
��
������C���˶���D��Ĺ��̣��ɻ�е���غ㶨�ɵã�
![]() ��
��
�������ݣ��������vC=5m/s��
�𣺻����˶���C��ʱ�ٶ�vc�Ĵ�СΪ5m/s��
��2���⣺������C���ٶȵ���ֱ����Ϊ��vy=vcsin��=3m/s��
B��C����ĸ߶Ȳ�Ϊh= ![]() ��
��
������B�˶���C���õ�ʱ��Ϊ ![]() ��
��
�����˶���B����ٶ�ΪvB=vCcos��=4m/s��
B��C���ˮƽ����x=vBt1=4��0.3m=1.2m��
��B��C����ĸ߶Ȳ�h��ˮƽ����xΪ1.2m��
��3���⣺������A���˶�B��Ĺ��̣��ɶ��ܶ����ã�
Pt�� ![]()
�������ݽ��t=0.4s��
��ˮƽ���������ڻ����ϵ�ʱ��tΪ0.4s��
����������1������ţ�ٵڶ�������������˶���D����ٶȣ���C��D�Ĺ������û�е���غ㶨�����C����ٶȣ���2����C����ٶȷֽ�Ϊˮƽ�������ֱ�����ƽ���ı��ζ��������ֱ���ٶȣ��Ӷ��ó�ƽ���˶���ʱ�䣬���ˮƽ���ٶȺ�ʱ�����ˮƽλ�ƣ�����3����A��B�Ĺ������ö��ܶ�������������õ�ʱ�䣮