题目内容
如图,两根足够长的光滑固定平行金属导轨与水平面成θ角,导轨间距为d,两导体棒a和b与导轨垂直放置,两根导体棒的质量都为m、电阻都为R,回路中其余电阻不计。整个装置处于垂直于导轨平面向上的匀强磁场中,磁感应强度的大小为B,在t=0时刻使a沿导轨向上作速度为v的匀速运动,同时将b由静止释放,b经过一段时间后也作匀速运动。已知d=1m,m=0.5kg,R=0.5Ω,B=0.5T,θ=300,g取10m/s2,不计两导棒间的相互作用力。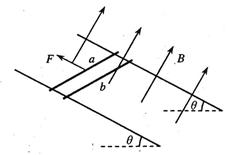
(1)若使导体棒b静止在导轨上,导体棒a向上运动的速度v多大?
(2)若a在平行于导轨向上的力F作用下,以v1=2m/s的速度沿导轨向上匀速运动,试导出F与b的速率v2的函数关系式并求出v2的最大值;
⑴10m/s ⑵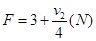 8m/s
8m/s
解析试题分析:⑴设a的速度为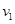 ,则
,则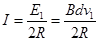 ①
①
对b: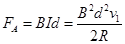 ②
② 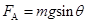 ③(1分)
③(1分)
将①②式代入③式得: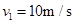 ④
④
⑵设a的速度为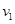 ,b的速度为
,b的速度为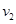 ,回路电流为I,
,回路电流为I,
则: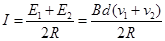 ⑤
⑤
对a: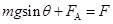
即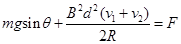 ⑥
⑥
代入数据得: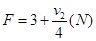
设b的最大速度为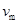 ,则有:
,则有: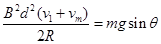
代入数据得: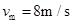
考点:导体切割磁感线时的感应电动势
点评:本题是电磁感应中的力学问题,综合运用电磁学知识和力平衡知识.对于第(2)问是两棒切割磁感线类型,要注意回路中感应电动势等于两棒产生的感应电动势之和.

练习册系列答案
相关题目


 (2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )
(2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )
