题目内容
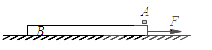
【题目】如图所示,可视为质点的物块A的质量为m=0.5 kg,完全相同的木板BC的长度均为L=2 m,质量为M=1.0 kg,物块A与木板之间的动摩擦因数为μ1=0.4,木板与地面间的动摩擦因数μ2=0.1,设物体与木板与地面间的最大静摩擦力与滑动摩擦力大小相等,重力加速度取g=10 m/s2,现给物块A一个初速度v0,物块在木板B上向右运动,要想使物块A能滑上木板C但又不能从C上滑下来,求初速度v0的取值范围(计算结果可保留根号)。
![]()
【答案】4 m/s<v0≤![]()
【解析】物块A在木板B上滑行时,它对木板B的摩擦力f1=μ1mg=0.4×0.5×10=2 N
物块A在木板B上滑行时,若木板相对于地面滑动,则地面对B的摩擦力:
f2=μ2(m+M+M)g=0.1×(0.5+1.0+1.0)×10=2.5 N>f1
所以木板相对于地面没有滑动
可知物块A刚好不能到达木板C时
f1L=0![]() mv02
mv02
代入数据得:v0=4 m/s
物块A刚好能到达木板C,则速度要满足:v0>4 m/s
当物块A滑上木板C后,受到木板C的摩擦力:摩擦力f3=μ1mg=0.4×0.5×10=2 N
当A在C板上滑行时地面对C的摩擦力:f4=μ2(m+M)g=0.1×(0.5+1.0)×10=1.5 N<f1
可知物块A在C上减速运动的过程中,木板C做匀加速直线运动
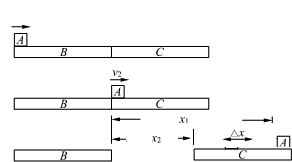
运动情况如右图所示
当物块A在B板上运动时,B、C板均相对地面不动,A做匀减速直线运动,其加速度![]()
设A滑上C板时的速度为v1,有![]()
当物块A在C板上运动时,B板留在原地,C板开始做匀加速运动,A继续做匀减速运动,A的加速度不变,当它们达到共同速度v2时,A相对C静止
设这段时内C的加速度为a2,由于木板C水平方向受到物块的摩擦力和地面的摩擦力,根据牛顿第二定律有:f3–f4=Ma2
所以:a2=0.5 m/s2
设这段时间内,A的位移为x1,C的位移为x2,则
对A:![]() ,
,![]()
对C:![]() ,
,![]()
又由它们的位移关系:x1–x2=Δx=L
可求得![]() ,
,![]() ,
,![]()
所以,若物块A恰好滑到木板C的右端,则对应的最大速度是![]()
故要想使物块A能滑上木板C但又不能从C上滑下来,初速度v0的取值范围为:4 m/s<v0≤![]()