题目内容
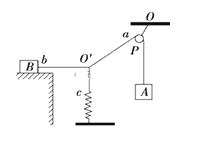
【题目】如图所示,质量分布均匀的小球,质量为m,半径为R;倾角α=45°的斜面体质量为M,放置在水平面上.在水平推力作用下,使斜面体底角刚好与墙角接触,撤去推力后小球和斜面体均做匀加速直线运动,直到小球恰好落地.不计一切摩擦,重力加速度为g.(tan22.5°=![]() )求:
)求:
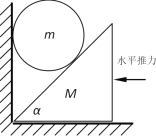
(1)静止时,水平推力F;
(2)撤去推力后,小球重力势能的变化量;
(3)撤去推力后,斜面体匀加速运动的时间.
【答案】(1)mg(2)-![]() mgR(3)
mgR(3)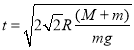
【解析】
(1)对小球受到重力mg、墙壁的弹力F1、斜面体的支持力F2.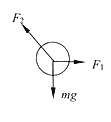
由平衡条件得
F1=mgtanα=mg
再对整体重力(m+M)g、地面的支持力FN、墙壁的弹力F1、水平推力F
对整体,由平衡条件得
F=F1=mg
(2)撤去推力后,小球重力势能的变化量
△Ep=-mg△h
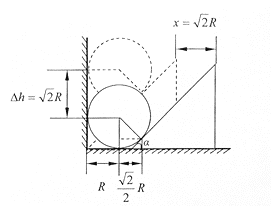
如图所示,由几何关系得到小球的重心位置下降了△h=2Rcos45°=![]() R,所以
R,所以
△Ep=-mg△h=-![]() mgR
mgR
(3)撤去水平推力F后小球竖直向下加速运动,斜面体水平向右加速运动,设加速度分别为a1和a2.根据牛顿第二定律得
对小球有
mg-F0cosα=ma1
对斜面体有
F0sinα=Ma2
两者的关系为
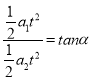
可得
![]()
由几何关系得到斜面体发生的位移
x=2Rcos45°
又 x=![]() a2t2解得
a2t2解得
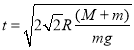

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目