题目内容
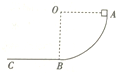
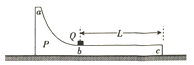
【题目】物体P静止在光滑水平地面上，其截面如图所示，图中ab段为光滑圆弧面，bc段是长度为L的粗糙的水平面，质量为物体P的一半的物块Q（可视为质点）从圆弧面的底端b以大小为v0的速度滑上圆弧面，并最终相对P静止在水平面的右端c．重力加速度大小为g．求：
（1）Q到达最高点时的速度大小v；
（2）Q与水平面间的动摩擦因数μ。
【答案】（1）
；（2）
【解析】
（1）木块Q从b运动到斜面上最高点的过程中，木块Q与物体P组成的系统，水平方向不受外力，水平方向的动量守恒。木块在最高点时，两者有共同速度，由动量守恒定律求解v。
（2）结合能量守恒定律求出Q与水平面间的动摩擦因数μ。
（1）设Q的质量为m，则P的质量为2m。木块Q在最高点时和P具有相同的速度。取水平向左为正方向，由系统水平方向动量守恒得：
mv0＝（m+2m）v
得：v＝
（2）经分析可知，Q最终相对P静止在c处时，它们的速度也为v．由能量守恒定律得：
mv02＝（m+2m）v2+μmgL
解得：μ＝
练习册系列答案
阅读快车系列答案
相关题目
