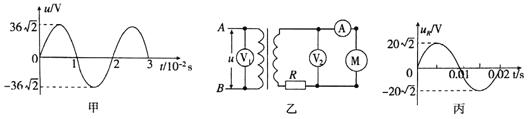
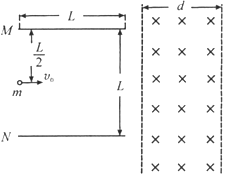
题目内容
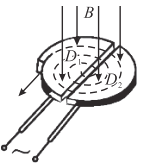
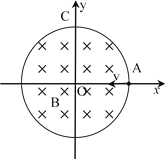
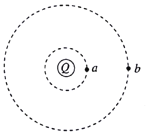
【题目】如图所示,正电荷Q固定在圆心,另外两个完全相同的带电粒子a、b绕Q做匀速圆周运动,它们的圆轨道在同一平面内,绕行方向相同。带电粒子a的轨道半径是r,带电粒子b的轨道半径是4r,带电粒子a做圆周运动的周期是T,不计a、b重力和a、b之的作用力,某时刻a、b两带电粒子距离达到最近,则下列说法正确的是:
A. 此时若使带电粒子b加速运动,有可能与a发生碰撞
B. 此时带电粒子a的电势能比带电粒子b的电势能大
C. 从该时刻起到a、b间相距最远所经历的最短时间为方![]() T
T
D. 从该时刻起到a、b间相距最远所经历的最短时间为![]() T
T
【答案】C
【解析】
由题意知a、b均带负电,若b加速运动,则b做离心运动,可判断不会与a发生碰撞;根据负电荷在电势越高的地方电势能越小,可判断带电粒子a的电势能与带电粒子b的电势能的大小关系;由牛顿第二定律求得a、b的周期关系,相距最远时转过的圆心角至少相差![]() .
.
由题意知a、b均带负电,设带电量为q
A、若使带电粒子b加速运动,则b做离心运动,不会与a发生碰撞,故A错误;
B、由题意知φa>φb,而负电荷在电势越高的地方电势能越小,所以带电粒子a的电势能比带电粒子b的电势能小,故B错误;
C、D、由牛顿第二定律得:对a:![]() ,对b:
,对b:![]() ,解得:Tb=8Ta=8T,设相距最远所经历的最短时间为t,则
,解得:Tb=8Ta=8T,设相距最远所经历的最短时间为t,则![]() ,解得:
,解得:![]() ,故C正确,D错误.
,故C正确,D错误.
故选C.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目