题目内容
如图所示,在竖直平面内,AB为水平放置的绝缘粗糙轨道,CD为竖直放置的足够长绝缘粗糙轨道,AB与CD通过四分之一绝缘光滑圆弧形轨道平滑连接,圆弧的圆心为O,半径R=0.50 m,轨道所在空间存在水平向右的匀强电场,场强的大小E=1.0×104 N/C,现有质量m=0.20 kg,电荷量q=8.0×10-4 C的带电体(可视为质点),从A点由静止开始运动,已知sAB=1.0 m,带电体与轨道AB、CD间的动摩擦因数均为0.5.假定带电体与轨道之间的最大静摩擦力和滑动摩擦力相等.求:(g=10 m/s2)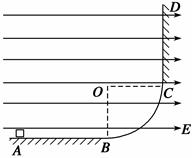
(1)带电体运动到圆弧形轨道C点时的速度;
(2)带电体最终停在何处.
(1) 10 m/s (2)与C点的竖直距离为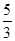 m处
m处
解析试题分析:(1)设带电体到达C点时的速度为v,
从A到C由动能定理得:qE(sAB+R)-μmg sAB-mgR=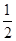 mv2 (3分)
mv2 (3分)
解得v=10 m/s(1分)
(2)设带电体沿竖直轨道CD上升的最大高度为h,从C到D由动能定理得:
-mgh-μqEh=0-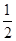 mv2(3分)
mv2(3分)
解得h=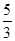 m(1分)
m(1分)
在最高点,带电体受到的最大静摩擦力Ffmax=μqE=4 N,
重力G=mg=2 N
因为G<Ffmax
所以带电体最终静止在与C点的竖直距离为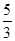 m处.(2分)
m处.(2分)
考点:本题考查考查带电体在电场中的运动,意在考查学生的综合分析能力。

练习册系列答案
相关题目
 ,sin370=0.6,cos370=0.8。
,sin370=0.6,cos370=0.8。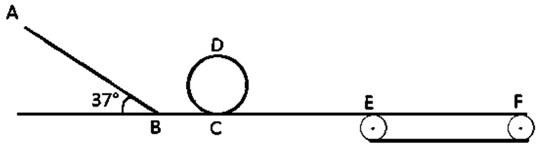
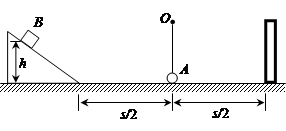
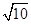 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求 
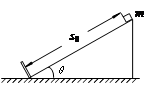

 。
。