题目内容
一轻质细绳一端系一质量为m=0.05kg的小球A,另一端挂在光滑水平轴O 上,O到小球的距离为L=0.1m,小球跟水平面接触,但无相互作用,在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,斜面与水平面平滑连接,如图所示,水平距离s=2m.现有一小滑块B,质量也为m,从斜面上滑下,与小球碰撞时交换速度,与挡板碰撞不损失机械能,与水平面间的动摩擦因数为μ=0.25.若不计空气阻力,并将滑块和小球都视为质点,g取10m/s2,试问: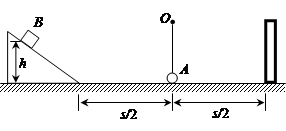
(1)若滑块B从斜面某一高度h处滑下与小球第一次碰撞后,使小球恰好在竖直平面内做圆周运动,求此高度h;
(2)若滑块B从h=5m处滑下,求滑块B与小球A第一次碰后瞬间绳子对小球的拉力;
(3)若滑块B从h="5m" 处下滑与小球A碰撞后,小球在竖直平面内做圆周运动,求小球做完整圆周运动的次数n.
(1)0.5m;(2)48N;(3)10
解析试题分析:(1)小球刚能完成一次完整的圆周运动,它到最高点的速度为v0,在最高点,仅有重力充当向心力,则有: (1分) ①
(1分) ①
在小球从h处运动到最高点的过程中,机械能守恒,则有: (2分) ②
(2分) ②
解上式有h=0.5m (1分)
(2)若滑块从 =5m处下滑到将要与小球碰撞时速度为
=5m处下滑到将要与小球碰撞时速度为 ,则有
,则有 ③ (1分)
③ (1分)
滑块与小球碰后的瞬间,同理滑块静止,小球以的速度开始作圆周运动,绳的拉力T和重力的合力充当向心力,则有  (1分) ④
(1分) ④
解④式得: T=48N (1分)
(3)滑块和小球第一次碰撞后,每在平面上经s路程后再次碰撞,则 (2分)
(2分)
解得:n=10次 (1分)
考点:机械能守恒定律、圆周运动、动能定理

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
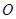 轴在竖直平面内无摩擦转动的细杆AB,两端分别固定质量1kg相等的两个球,已知OB=0.6m。现由水平位置自由释放,求:
轴在竖直平面内无摩擦转动的细杆AB,两端分别固定质量1kg相等的两个球,已知OB=0.6m。现由水平位置自由释放,求:
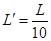 ,高度差为
,高度差为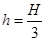 。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为
。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为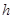 ,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。
,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。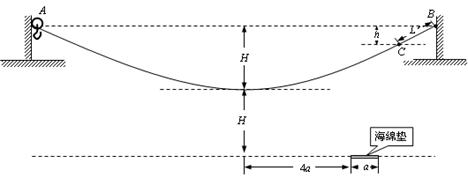
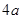 、宽度为
、宽度为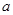 ,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?
,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?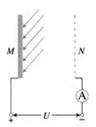
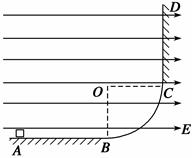
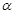 =53o,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取重力加速度
=53o,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取重力加速度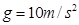 , (
, (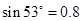 ,
,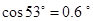 )
)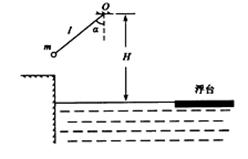
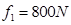 ,平均阻力
,平均阻力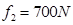 ,求选手落入水中的深度
,求选手落入水中的深度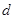 ;
;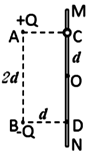

 ,P、Q两点的电势差为U,不计重力作用,求:
,P、Q两点的电势差为U,不计重力作用,求: