题目内容
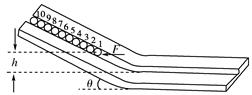
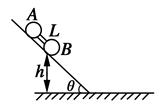
如图,半径为R的光滑圆形轨道安置在一竖直平面上,左侧连接一个光滑的弧形轨道,右侧连接动摩擦因数为μ的水平轨道CD.一小球自弧形轨道上端的A处由静止释放,通过圆轨道后,再滑上CD轨道.若在圆轨道最高点B处对轨道的压力恰好为零,到达D点时的速度为 。
。
求⑴小球经过B点时速度的大小
⑵小球释放时的高度h
⑶水平轨道CD段的长度l
(1)vB= (2)
(2) (3)
(3)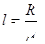
解析试题分析:⑴根据小球在B处对轨道压力为零,由向心力公式有: ① (2分)
① (2分)
解得小球、经过B点时速度大小vB= ②(2分)
②(2分)
⑵取轨道最低点为零势能点,由机械能守恒定律: ③ (2分)
③ (2分)
由②③联立解得 ④(2分)
④(2分)
⑶对小球从最高点到D点全过程应用动能定理有: ⑤(2分)
⑤(2分)
又vD= ⑥
⑥
有④⑤⑥联立解得: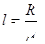
考点:本题考查动能定理和机械能守恒定律,涉及圆周运动的临界问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
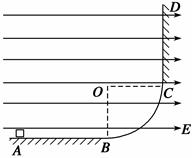
 是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴
是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴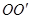 匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为
匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为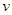 .已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求:
.已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求: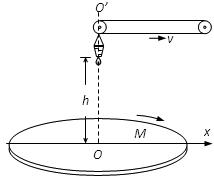
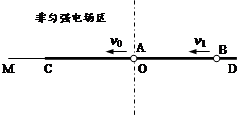
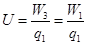
 ,P、Q两点的电势差为U,不计重力作用,求:
,P、Q两点的电势差为U,不计重力作用,求: