题目内容
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(1)求把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功.
(2)求小球B运动到C处时所受的向心力的大小.
(3)问小球B被拉到离地多高时滑块A与小球B的速度大小相等?
(1)求把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功.
(2)求小球B运动到C处时所受的向心力的大小.
(3)问小球B被拉到离地多高时滑块A与小球B的速度大小相等?

(1)
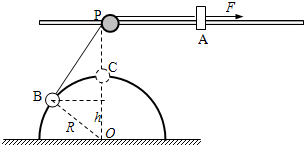
对于F的做功过程,由几何知识有
=
=
=0.5m
=
-R=0.4-0.3=0.1m
则力F做的功W=F?(
-
)
所以,W=60×(0.5-0.1)=24J.
(2)由于B球到达C处时,已无沿绳的分速度,所以此时滑块A的速度为零,
考察两球及绳子组成的系统的能量变化过程,由功能关系,得
W=
mv2+mgR
代入已知量,得 24=
×3×v2+3×10×0.3
解得v=
m/s
因为向心力公式为F=m
所以,代入已知量,得F=3×
=100N
(3)当绳与轨道相切时两球速度相等,
由相似三角形知识,得
=
代入已知量,得
=
所以,h=
=0.225m
答:
(1)把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功为24J.
(2)小球B运动到C处时所受的向心力的大小是100N.
(3)小球B被拉到离地0.225m高时滑块A与小球B的速度大小相等.

对于F的做功过程,由几何知识有
| . |
| PB |
|
| 0.42+0.32 |
| . |
| PC |
| . |
| PO |
则力F做的功W=F?(
| . |
| PB |
| . |
| PC |
所以,W=60×(0.5-0.1)=24J.
(2)由于B球到达C处时,已无沿绳的分速度,所以此时滑块A的速度为零,
考察两球及绳子组成的系统的能量变化过程,由功能关系,得
W=
| 1 |
| 2 |
代入已知量,得 24=
| 1 |
| 2 |
解得v=
| 10 |
因为向心力公式为F=m
| v2 |
| R |
所以,代入已知量,得F=3×
| ||
| 0.3 |
(3)当绳与轨道相切时两球速度相等,
由相似三角形知识,得
| ||
| R |
| R |
| h |
代入已知量,得
| 0.4 |
| 0.3 |
| 0.3 |
| h |
所以,h=
| 9 |
| 40 |
答:
(1)把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功为24J.
(2)小球B运动到C处时所受的向心力的大小是100N.
(3)小球B被拉到离地0.225m高时滑块A与小球B的速度大小相等.

练习册系列答案
相关题目
 (2007?海淀区一模)如图所示,在距水平地面高h=0.80m的水平桌面一端的边缘放置一个质量m=0.80kg的木块B,桌面的另一端有一块质量M=1.0kg的木块A以初速度v0=4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上.木块B离开桌面后落到地面上的D点.设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数μ=0.25,重力加速度取g=10m/s2.求:
(2007?海淀区一模)如图所示,在距水平地面高h=0.80m的水平桌面一端的边缘放置一个质量m=0.80kg的木块B,桌面的另一端有一块质量M=1.0kg的木块A以初速度v0=4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上.木块B离开桌面后落到地面上的D点.设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数μ=0.25,重力加速度取g=10m/s2.求: (2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: 如图所示,在距水平地面高为h处有一半径为R的1/4圆弧轨道,圆弧轨道位于竖直平面内,轨道光滑且末端水平,在轨道的末端静置一质量为m的小滑块A.现使另一质量为m的小滑块B从轨道的最高点由静止释放,并在轨道的最低点与滑块A发生碰撞,碰后粘合为一个小滑块C已知重力加速度为g.求:
如图所示,在距水平地面高为h处有一半径为R的1/4圆弧轨道,圆弧轨道位于竖直平面内,轨道光滑且末端水平,在轨道的末端静置一质量为m的小滑块A.现使另一质量为m的小滑块B从轨道的最高点由静止释放,并在轨道的最低点与滑块A发生碰撞,碰后粘合为一个小滑块C已知重力加速度为g.求: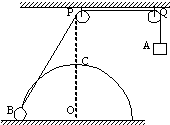 如图所示,在距水平地面高均为0.4m处的P、Q两处分别固定两光滑小定滑轮,细绳跨过滑轮,一端系一质量为mA=2.75kg的小物块A,另一端系一质量为mB=1kg的小球B.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,且与两滑轮在同一竖直平面内,小球B套在轨道上,静止起释放该系统,则小球B被拉到离地
如图所示,在距水平地面高均为0.4m处的P、Q两处分别固定两光滑小定滑轮,细绳跨过滑轮,一端系一质量为mA=2.75kg的小物块A,另一端系一质量为mB=1kg的小球B.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,且与两滑轮在同一竖直平面内,小球B套在轨道上,静止起释放该系统,则小球B被拉到离地 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取