题目内容
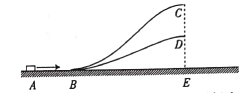
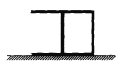
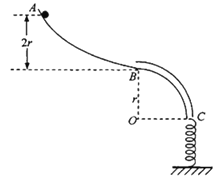
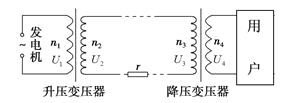
【题目】竖直平面内有固定的半径R=0.15m的光滑半圆轨道COD，圆心O下方有水平向右的匀强电场，上方无电场，传送带AB以很大的速度逆时针转动，左端B与圆形轨道上端C在同一竖直线上。带电滑块（m，+q）与传送带间的摩擦因数μ=0.1，将滑块无初速度从A端释放，滑块滑过传送带后恰好可以沿着圆形轨道内侧运动，然后滑上静止于粗糙地面上的木板M，已知m=1kg，M=2kg，M的长度l2=1.8m，重力加速度g=10m/s2，电场强度
，M、m之间的摩擦因数μ1=0.7，M与地面之间的摩擦因数为μ2=1/6，木板右端与固定挡板之间的初始距离PQ为l3，滑块和木板撞到固定挡板速度都会立即变为零。求：
（1）传送带的长度l1；
（2）滑块刚滑上木板时的速度；
（3）滑块滑到D点后M、m之间的摩擦生热。
【答案】（1）0.75m（2）3m/s（3）若L3>0.5m，Q=12.25J；若0.45m<L3<0.5m，(15.75-7L3)J；若L3<0.45m，Q=12.6J
【解析】
根据“圆心O下方有水平向右的匀强电场”可知，本题考查的是匀强电场下的动力学分析问题，根据匀变速直线运动的规律、动能定理、动力学规律，列式即可。
（1）传送带的速度很大，物块恰好沿光滑圆弧轨道运动，所以可知物块一直匀加速到达B点，且
，可得
；
（2）根据动能定理可得
，滑块刚滑上木板时的速度vD=3m/s；
（3）以向右为正方向，滑块滑上长木板以后，滑块的加速度
，长木板的加速度
，共速以后，由于
，两者一起匀速。作出两者的速度时间图像如图所示。
通过分析发现，共速时的相对位移等于1.5m，小于长木板长度，所以滑块不会掉下去。
①若L3>0.5m，则M、m共速后M撞上挡板，此时m单独减速，减到0的位移等于0.25m<0.3m，m不会撞到挡板，M、m之间的相对位移等于（1.5+0.25）m=1.75m，M、m之间的摩擦热Q=12.25J
②若M、m共速前M撞上挡板，此时m一直减速，此时m减速的总位移为2.25m，求得L3=0.45m，所以如果L3<0.45m，m会撞到挡板，M、m之间的相对位移等于1.8m，M、m之间的摩擦热Q=12.6J，如果0.45m<L3<0.5m，m不会撞到挡板，M、m之间的相对位移等于（2.25-L3）m，M、m之间的摩擦热Q=（15.75-7L3）J
