题目内容
 质量为2.0×103kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×106N.汽车经过半径为50m的弯路时,车速达到72km/h.
质量为2.0×103kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×106N.汽车经过半径为50m的弯路时,车速达到72km/h.(1)请你通过计算说明这辆车会不会发生侧滑;
(2若将公路转弯处路面设计成外侧高、内侧低,当汽车以36km/h的速率转弯时,恰好使车与路面间无摩擦力.求路面与水平面倾角a的正切值.
分析:(1)汽车做圆周运动,重力与支持力平衡,侧向静摩擦力提供向心力,可求出所需向心力与侧向最大静摩擦力比较,即可判断;
(2)若将公路转弯处路面设计成外侧高、内侧低,当汽车以36km/h的速率转弯时,恰好使车与路面间无摩擦力,由路面的支持力和重力的合力提供向心力,根据牛顿第二定律求解.
(2)若将公路转弯处路面设计成外侧高、内侧低,当汽车以36km/h的速率转弯时,恰好使车与路面间无摩擦力,由路面的支持力和重力的合力提供向心力,根据牛顿第二定律求解.
解答:解:(1)汽车转弯的速度为:v=72km/h=20m/s
汽车转弯时做圆周运动,所需要的向心力为:Fn=m
=2.0×103×
N=1.6×104N
而汽车所受的最大静摩擦力为fm=1.4×106N,则Fn>fm,所以汽车会做离心运动,发生侧滑;
(2)若将公路转弯处路面设计成外侧高、内侧低,当汽车以v′=36km/h=10m/s的速率转弯时,恰好使车与路面间无摩擦力,由路面的支持力和重力的合力提供向心力,根据牛顿第二定律得:
mgtanα=m
得:tanα=
=
=0.2
答:(1)通过计算知道这辆车会发生侧滑;
(2)路面与水平面倾角a的正切值为0.2.
汽车转弯时做圆周运动,所需要的向心力为:Fn=m
| v2 |
| R |
| 202 |
| 50 |
而汽车所受的最大静摩擦力为fm=1.4×106N,则Fn>fm,所以汽车会做离心运动,发生侧滑;
(2)若将公路转弯处路面设计成外侧高、内侧低,当汽车以v′=36km/h=10m/s的速率转弯时,恰好使车与路面间无摩擦力,由路面的支持力和重力的合力提供向心力,根据牛顿第二定律得:
mgtanα=m
| v2 |
| R |
得:tanα=
| v2 |
| gR |
| 102 |
| 10×50 |
答:(1)通过计算知道这辆车会发生侧滑;
(2)路面与水平面倾角a的正切值为0.2.
点评:本题关键找出向心力来源,将侧向最大静摩擦力与所需向心力比较,若静摩擦力不足提供向心力,则车会做离心运动.第二问类似于圆锥摆,难度不大.

练习册系列答案
相关题目
 如图所示,一辆质量为 2.0×103 kg 的汽车在平直公路上行驶,若汽车行驶过程中所受阻力恒为f=2.5×103N,且保持功率为 80kw 求:
如图所示,一辆质量为 2.0×103 kg 的汽车在平直公路上行驶,若汽车行驶过程中所受阻力恒为f=2.5×103N,且保持功率为 80kw 求:
 辆质量为2.0×103
辆质量为2.0×103 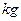 的汽车以额定功率为
的汽车以额定功率为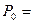 6.0×104
6.0×104 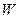 在水平公路上行驶,汽车受到的阻力为一定值,在某时刻汽车的速度为
在水平公路上行驶,汽车受到的阻力为一定值,在某时刻汽车的速度为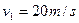 ,加速度为
,加速度为 ,求(g取
,求(g取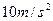 ):
): 是多大?
是多大? ,则这一过程能保持多长时间?
,则这一过程能保持多长时间?