题目内容
如图,地球赤道上山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动。设e、p、q的圆周运动速率分别为v1、v2、v 3,向心加速度分别为a1、a2、a3,则( )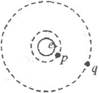
| A.v1>v2>v 3 | B.v1<v3<v 2 |
| C.a1>a2>a3 | D.a1<a2<a3 |
B
解析试题分析:由图可知,三者所做圆周运动的轨道半径关系为:r3>r2>r1,由于地球同步卫星与地球自转具有相同的角速度,即:ω3=ω1,根据匀速圆周运动参量关系v=rω和a=vω有:v3>v1、a3>a1,故选项A、C错误;又因为地球近地卫星和地球同步卫星所做圆周运动的向心力均有地球对它们的万有引力提供,根据万有引力定律和牛顿第二定律有: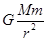 =
=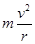 =ma,解得:v=
=ma,解得:v=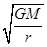 、a=
、a=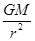 ,因此有:v2>v3、a2>a3,所以:v2>v3>v1、a2>a3>a1,故选项D错误;选项B正确。
,因此有:v2>v3、a2>a3,所以:v2>v3>v1、a2>a3>a1,故选项D错误;选项B正确。
考点:本题主要考查了圆周运动参量关系和卫星运行参量与轨道半径的关系问题,属于中档题。

一质点沿螺旋线自外向内运动,如图所示。已知其走过的弧长s与时间t的一次方成正比。则关于该质点的运动下列说法正确的是( )
| A.小球运动的线速度越来越大 |
| B.小球运动的加速度越来越大 |
| C.小球运动的角速度越来越大 |
| D.小球所受的合外力不变 |
如图所示,内壁光滑的半球形容器固定放置,其圆形顶面水平。两个完全相同的小球a、b分别沿容器内壁,在不同的水平面内做匀速圆周运动。下列判断正确的是
| A.a对内壁的压力小于b对内壁的压力 |
| B.a的周期小于b的周期 |
| C.a的角速度小于b的角速度 |
| D.a的向心加速度与b的向心加速度大小相等 |
如图所示,质量相同的两个小球,分别用长l和2l的细绳悬挂在天花板上。分别拉起小球使细绳伸直呈水平状态,然后轻轻释放,不计任何阻力作用。当小球到达最低位置时( )
| A.两球运动的线速度相等 |
| B.两球运动的角速度相等 |
| C.两球的向心加速度相等 |
| D.细绳对两球的拉力相等 |
如图所示,一质量为m的质点,在一无摩擦的半径为R的竖直环形细圆管轨道上运动,通过最高点时的速度为 ,g是重力加速度,则下列叙述正确的是
,g是重力加速度,则下列叙述正确的是
| A.质点运动过程中机械能守恒 |
B.质点运动的最大速率为 |
| C.在最高点处,轨道对质点作用力的大小为0.8mg |
| D.在任一条直径的两个端点上,质点的动能之和不变 |
轻杆一端固定在光滑水平轴O上,另一端固定一质量为m的小球,如图所示.给小球一初速度,使其在竖直平面内做圆周运动,且刚好能通过最高点P,下列说法正确的是( )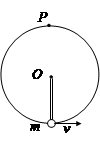
| A.小球在最高点时对杆的作用力为零 |
| B.小球在最高点时对杆的作用力为mg |
| C.若增大小球的初速度,则在最高点时球对杆的力一定增大 |
| D.若增大小球的初速度,则在最高点时球对杆的力可能为零 |






 向右匀速运动的小车的顶部,两球恰与小车前后壁接触,由于某种原因,小车突然停止运动,此时悬线的拉力之比FB∶FA为(
向右匀速运动的小车的顶部,两球恰与小车前后壁接触,由于某种原因,小车突然停止运动,此时悬线的拉力之比FB∶FA为( )
) 