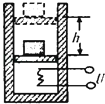
��Ŀ����
����Ŀ�����ʹ��Ժ㶨�ٶ�v=4m/s˳ʱ�����У����ʹ���ˮƽ��ļнǦ�=37�㣬�ֽ�����m=2kg��С��Ʒ�������ˣ�С��Ʒ�ɿ����ʵ㣩��ƽ̨�ϵ���ͨ��һ�������ú���F=20N��С��Ʒ������һ��ʱ����Ʒ��������ظ�ΪH=1.8m��ƽ̨�ϣ���ͼ��ʾ����֪��Ʒ�봫�ʹ����Ķ�Ħ��������=0.5�������Ħ�������ڻ���Ħ������gȡ10m/s2 �� ��֪sin37��=0.6��cos37��=0.8��
����Ʒ�Ӵ��ʹ����˶���ƽ̨�����õ�ʱ���Ƕ��٣����ʹ����������˶��ٹ���
��������Ʒ�봫�ʹ��ﵽ��ͬ�ٶ�˲�䳷ȥ����F������Ʒ�������ʱ���뿪Ƥ����������뿪Ƥ��ʱ���ٶȣ�
���𰸡��⣺����Ʒ�ڴﵽ�봫�ʹ��ٶ�v=4m/s���ǰ����ţ�ٵڶ������У�
F+��mgcos37�㩁mgsin37��=ma1
��� a1=8m/s2
��v=a1t1 �� �� t1=0.5s
� x1= ![]() a1t12=1m��
a1t12=1m��
����У�F����mgcos37�㩁mgsin37��=ma2
��� a2=0������Ʒ�洫�ʹ���������
� x2= ![]() ��x1=2m
��x1=2m
t2= ![]() =0.5s
=0.5s
��ʱ��Ϊ��t=t1+t2=1s
����Ʒ�Ӵ��ʹ����˶���ƽ̨�����õ�ʱ����1s��
���������غ㶨�ɵã�WF+W= ![]() +mgH
+mgH
���Դ��ʹ���С��������Ĺ�Ϊ
W= ![]() +mgH��F
+mgH��F ![]()
= ![]() +20��1.8��20��
+20��1.8��20�� ![]() =��8J
=��8J
������Ʒ�봫�ʹ��ﵽͬ��˲�䳷ȥ����F������ţ�ٵڶ����ɣ���
��mgcos37�㩁mgsin37��=ma3
��ã�a3=��2m/s2��
������Ʒ�����ȼ��ٵ��ٶ�Ϊ��ʱ��ͨ����λ��Ϊx
x=�� ![]() =4m��x2��
=4m��x2��
�������ٶ�Ϊ��Ϊ��ʱ�Ѿ�������ߵ㣻
��x2=vt3+ ![]() a3t32��
a3t32��
��� t3=��2�� ![]() ��s��t3=��2+
��s��t3=��2+ ![]() ��s��0.5s����ȥ����
��s��0.5s����ȥ����
���ﶥ�˵��ٶ� v��=v��a3t3=4��2����2�� ![]() ��=2m/s��������б������
��=2m/s�������������
��
����Ʒ�Ӵ��ʹ����˶���ƽ̨�����õ�ʱ����1s�����ʹ����������˩�8J����
��������Ʒ�봫�ʹ��ﵽ��ͬ�ٶ�˲�䳷ȥ����F����Ʒ���裨2�� ![]() ��sʱ���뿪Ƥ��������뿪Ƥ��ʱ���ٶ���2m/s��������б������
��sʱ���뿪Ƥ��������뿪Ƥ��ʱ���ٶ���2m/s��������б������
�����������ȼ��贫�ʹ��㹻�����Ի�����������������ţ�ٵڶ������������ٶȣ�Ȼ�������˶�ѧ��ʽ�������ٵ�λ�ƺ�ʱ�䣬����λ���ж��Ƿ��еڶ������̣����ٶȵ��ڴ��ʹ��ٶȺ�ͨ���������������Եó�����ǡ�������ϻ������õ���ʱ�䣻���������غ㶨�����ʹ����������Ĺ���
��������Ʒ�봫�ʹ��ﵽͬ��˲�䳷ȥ����F������������������ţ�ٵڶ�����������ٶȣ�Ȼ������˶�ѧ��ʽ��ʽ��⣮

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�