题目内容
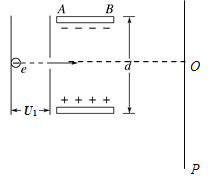
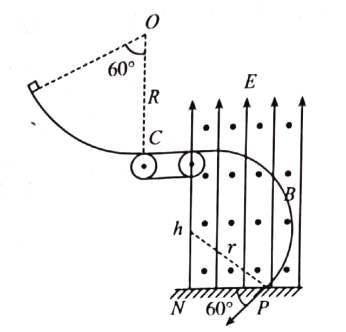
【题目】如图所示,半径R=3.6m的![]() 光滑绝缘圆弧轨道,位于竖直平面内,与长L=5m的绝缘水平传送带平滑连接,传送带以v=5m/s的速度顺时针转动,传送带右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=20N/C,磁感应强度B=2.0T,方向垂直纸面向外。a为m1=1.0×10-3kg的不带电的绝缘物块,b为m2=2.0×10-3kg、q=1.0×10-3C带正电的物块。B静止于圆弧轨道最低点,将a物块从圆弧轨道顶端由静止释放,运动到最低点与b发生弹性碰撞(碰后b的电荷量不发生变化)。碰后b先在传送带上运动,不离开传送带飞入复合场中,最后以速度方向与水平变成60°角落在地面上的P点(如图),已知b物块与传送带之间的动摩擦因数为μ=0.1.(g取10m/s2,a、b均可看作质点)求:
光滑绝缘圆弧轨道,位于竖直平面内,与长L=5m的绝缘水平传送带平滑连接,传送带以v=5m/s的速度顺时针转动,传送带右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=20N/C,磁感应强度B=2.0T,方向垂直纸面向外。a为m1=1.0×10-3kg的不带电的绝缘物块,b为m2=2.0×10-3kg、q=1.0×10-3C带正电的物块。B静止于圆弧轨道最低点,将a物块从圆弧轨道顶端由静止释放,运动到最低点与b发生弹性碰撞(碰后b的电荷量不发生变化)。碰后b先在传送带上运动,不离开传送带飞入复合场中,最后以速度方向与水平变成60°角落在地面上的P点(如图),已知b物块与传送带之间的动摩擦因数为μ=0.1.(g取10m/s2,a、b均可看作质点)求:

(1)物块a运动到圆弧轨道,最低点时的速度大小及碰后b的速度大小;
(2)b离开传送带右端时的速度大小及从开始运动到落地瞬间所用时间;
(3 )若撤掉匀强磁场,使匀强电场的方向竖直向下,则b离开传送带飞入电场中,最后落在地面上的 Q点,请判断Q点位于P点的左侧、右侧还是与P点重合。
【答案】(1) 4 m/s(2) 3.2s(3) Q点与P点重合
【解析】
(1)a物块从释放到运动到圆弧轨道最低点C时,
由动能定理有
m1gR(l-cos![]() )=
)=![]()
解得
vC= 6 m/s
碰撞过程,取水平向右为正方向,由动量守恒定律有
m1vC=m1v′C+m2vb
a、b弹性碰撞,由能量守恒有
![]() =
=![]() +
+![]()
解得
vb=4 m/s
(2)b在传送带上假设能与传送带达到共速时经过的位移为s,
则
μm2g=m2a,
v2-vb2= 2as
得
s=4.5 m<L
则b在传送带上先匀加速后匀速,匀加速时间
T=![]() =1s
=1s
匀速运动时间
t′=![]() =0.1s
=0.1s
在传送带上运动时间为
t1=t+t′=1.1s
所以b离开传送带时速度为v= 5 m/s,b进入复合场后,有
qE=m2g= 2×10-2 N
所以物块b在复合场中做匀速圆周运动
b在磁场中运动的周期
T=![]()
则运动的时间为
t2=![]()
b从开始运动到落地的瞬间所用时间为
t1+t2=(1.1+![]() )s≈3.2s
)s≈3.2s
(3)b进入复合场后,有
qE=m2g=2×10-2 N
所以b做匀速圆周运动
由 qvB=![]() 解得
解得
r=![]() =5m
=5m
由几何知识解得传送带上边与水平地面的高度
h=r+![]() =7.5 m
=7.5 m
若撤掉匀强磁场,使匀强电场的方向竖直向下,则粒子在电场中做类平抛运动
竖直方向
qE+m2g=m2a2,
h=![]()
解得
tE=![]() s
s
NQ=vtE=![]() m
m
在电场和磁场重合区域,根据几何关系得
NP=rsin50°=![]() m
m
则PQ=0,即Q点与P点重合。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案