题目内容
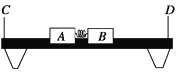
【题目】如图所示，有一内表面光滑的金属盒，底面长为L=1.2m，质量为m1=1kg，放在水平面上，与水平面间的动摩擦因数为μ=0.2，在盒内最右端放一半径为r=0.1m的光滑金属球，质量为m2=1kg，现在盒的左端，给盒一个初速度v=3m/s（盒壁厚度，球与盒发生碰撞的时间和能量损失均忽略不计，g取10m/s2）求：金属盒从开始运动到最后静止所经历的时间?
【答案】0.75s
【解析】
试题分析：根据动能定理，则从开始运动到左壁与小球相碰有：
解得盒与球第一次碰撞速度v1=1m/s
此过程经历的时间为：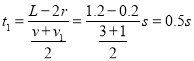
由于小球和盒子发生弹性碰撞，故碰撞完后交换速度，即小球速度为1m/s，盒子速度为零
此后小球在盒内的运动时间为：
小球与盒子再次相碰后，再次交换速度，盒子速度为1m/s，小球速度为零，则由动量定理可知盒子运动的时间t3满足：
，解得t3=0.25s
则金属盒从开始运动到最后静止所经历的时间为 t=t1+t2+t3=1.75s
练习册系列答案
相关题目
