题目内容
在倾角为30°的光滑斜面上,一小球从A点由静止释放经时间t0到达B点,另一个小球从A点水平抛出,落点也在B点,从以上情况可知( )
分析:根据牛顿第二定律求出小球从斜面滑下的加速度,由位移求出A到B的位移大小.根据两球的位移相同,则可求出另一小球下落的高度.根据平抛运动竖直方向是自由落体运动,由高度求出时间.由水平方向的匀速运动,求出初速度.
解答:解:设A到B的距离为S.
小球从斜面滑下的加速度大小为a=gsin30°,
则:s=
a
=
g
对于平抛运动的小球,设运动时间为t,则
ssin30°=
gt2
联立解得:t=
t0,
初速度 v 0=
=
gt0
故ABD错误,C正确;
故选:C
小球从斜面滑下的加速度大小为a=gsin30°,
则:s=
| 1 |
| 2 |
| t | 2 0 |
| 1 |
| 4 |
| t | 2 0 |
对于平抛运动的小球,设运动时间为t,则
ssin30°=
| 1 |
| 2 |
联立解得:t=
| 1 |
| 2 |
初速度 v 0=
| scos30° |
| t |
| ||
| 4 |
故ABD错误,C正确;
故选:C
点评:本题首先要抓住两个运动的关系:位移相同,其次抓住平抛运动的研究方法:运动的分解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如题所示,在倾角为30°的光滑斜面上端系有一劲度系数为200N/m的轻质弹簧,弹簧下端连一个质量为2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以4m/s2的加速度沿斜面向下做匀加速运动,取g=10m/s2,则( )
如题所示,在倾角为30°的光滑斜面上端系有一劲度系数为200N/m的轻质弹簧,弹簧下端连一个质量为2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以4m/s2的加速度沿斜面向下做匀加速运动,取g=10m/s2,则( )| A、小球从一开始就与挡板分离 | B、小球速度最大时与挡板分离 | C、小球向下运动0.01m时与挡板分离 | D、小球向下运动0.02m时速度最大 |
 如图所示,在倾角为α=30°的光滑斜面上,有一根长为L=0.8m的细绳,一端固定在O点,另一端系一质量为m=0.2kg的小球,沿斜面做圆周运动,若要小球能通过最高点A,则小球在最低点B的最小速度是( )
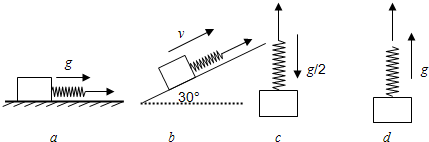
如图所示,在倾角为α=30°的光滑斜面上,有一根长为L=0.8m的细绳,一端固定在O点,另一端系一质量为m=0.2kg的小球,沿斜面做圆周运动,若要小球能通过最高点A,则小球在最低点B的最小速度是( ) 质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为( )
质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为( ) 在倾角为30°的光滑斜面上有相距40m的两个可看作质点的小物体P和Q,质量分别mP=0.1kg和mQ=0.5kg,其中P不带电,Q带电.整个装置处在正交的匀强电场和匀强磁场中,电场强度的大小为50V/m,方向竖直向下;磁感应强度的大小为5πT,方向垂直纸面向里.开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移).碰撞后,两物体能够再次相遇.斜面无限长,g取10m/s2.求:
在倾角为30°的光滑斜面上有相距40m的两个可看作质点的小物体P和Q,质量分别mP=0.1kg和mQ=0.5kg,其中P不带电,Q带电.整个装置处在正交的匀强电场和匀强磁场中,电场强度的大小为50V/m,方向竖直向下;磁感应强度的大小为5πT,方向垂直纸面向里.开始时,将小物体P无初速释放,当P运动至Q处时,与静止在该处的小物体Q相碰,碰撞中Q的电荷量保持不变(即不转移).碰撞后,两物体能够再次相遇.斜面无限长,g取10m/s2.求: