题目内容
 质量为M的小车,静止在光滑的水平面上,现有一个质量为m的小铁块,以初速度v0从左端滑上小车,如图所示,铁块与小车间的动摩擦因数为μ,求:
质量为M的小车,静止在光滑的水平面上,现有一个质量为m的小铁块,以初速度v0从左端滑上小车,如图所示,铁块与小车间的动摩擦因数为μ,求:(1)若铁块不会从小车上滑落,则铁块与小车相对静止时的速度为多大?
(2)若要铁块不会从小车上滑落,则小车的长度至少要多长?
(3)从铁块滑上小车到与小车相对静止的过程中,产生的内能为多少?
分析:(1)由于摩擦作用,滑块减速,平板小车加速,系统水平方向不受外力,总动量守恒,可求出相对静止时的共同速度;
(2)由功能关系,物块与小车之间一对滑动摩擦力做功之和(摩擦力乘以相对位移)等于系统机械能的增量,列出等式求解
(3)根据能量守恒列出等式求解
(2)由功能关系,物块与小车之间一对滑动摩擦力做功之和(摩擦力乘以相对位移)等于系统机械能的增量,列出等式求解
(3)根据能量守恒列出等式求解
解答:解:物块滑上小车后,受到向后的摩擦力而做减速运动,小车受到向前的摩擦力而做加速运动,因小车足够长,最终物块与小车相对静止,如图所示.由于“光滑水平面”,系统所受合外力为零,故满足动量守恒定律.
(1)由动量守恒定律,物块与小车系统:
mv0=( M+m )v
v=
(2)由功能关系,物块与小车之间一对滑动摩擦力做功之和(摩擦力乘以相对位移)等于系统机械能的增量:
-μmgL=
(M+m)v2-
m
L=
(3)根据能量守恒得产生的内能等于系统动能的损失,
所以Q=
m
-
(M+m)v2=
答:(1)若铁块不会从小车上滑落,则铁块与小车相对静止时的速度为
(2)若要铁块不会从小车上滑落,则小车的长度至少是
(3)从铁块滑上小车到与小车相对静止的过程中,产生的内能为
(1)由动量守恒定律,物块与小车系统:
mv0=( M+m )v
v=
| mv0 |
| M+m |
(2)由功能关系,物块与小车之间一对滑动摩擦力做功之和(摩擦力乘以相对位移)等于系统机械能的增量:
-μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
L=
| ||
| 2μg(M+m) |
(3)根据能量守恒得产生的内能等于系统动能的损失,
所以Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| ||
| 2(M+m) |
答:(1)若铁块不会从小车上滑落,则铁块与小车相对静止时的速度为
| mv0 |
| M+m |
(2)若要铁块不会从小车上滑落,则小车的长度至少是
| ||
| 2μg(M+m) |
(3)从铁块滑上小车到与小车相对静止的过程中,产生的内能为
| ||
| 2(M+m) |
点评:注意动量守恒的条件是如果一个系统不受外力或所受外力的矢量和为零,那么这个系统的总动量保持不变.灵活运用动量守恒定律、能量守恒列式求解.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

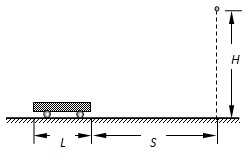 (2008?济南模拟)如图所示,质量为m的小车,静止在光滑的水平地面上,车长为L,现给小车施加一个水平向右的恒力F,使小车向右做匀加速运动,与此同时在小车的正前方S处的正上方H高处,有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),问恒力F满足什么条件小球可以落到小车上?
(2008?济南模拟)如图所示,质量为m的小车,静止在光滑的水平地面上,车长为L,现给小车施加一个水平向右的恒力F,使小车向右做匀加速运动,与此同时在小车的正前方S处的正上方H高处,有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),问恒力F满足什么条件小球可以落到小车上?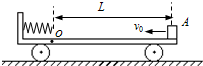 如图所示,质量为M的小车B静止在光滑水平面上,车的左端固定着一根弹簧,小车上O点以左部分光滑,O点以右部分粗糙,O点到小车右端长度为L.一质量为m的小物块A(可视为质点),以速度v0从小车右端向左滑动,与弹簧相碰,最后刚好未从小车右端滑出.求:
如图所示,质量为M的小车B静止在光滑水平面上,车的左端固定着一根弹簧,小车上O点以左部分光滑,O点以右部分粗糙,O点到小车右端长度为L.一质量为m的小物块A(可视为质点),以速度v0从小车右端向左滑动,与弹簧相碰,最后刚好未从小车右端滑出.求: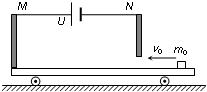 如图所示,在光滑的水平面上有质量为m的小车处于静止状态,车底板光滑绝缘,左右两块金属板M、N竖直固定在车上,它们间隔一定距离,在M、N间接上一定电压的电源,N接电源负极.现有一可看作质点的带正电荷的物块,质量为m0,电量为q,从N板的小孔以速度v0射入静止小车的两板间,求:
如图所示,在光滑的水平面上有质量为m的小车处于静止状态,车底板光滑绝缘,左右两块金属板M、N竖直固定在车上,它们间隔一定距离,在M、N间接上一定电压的电源,N接电源负极.现有一可看作质点的带正电荷的物块,质量为m0,电量为q,从N板的小孔以速度v0射入静止小车的两板间,求: