题目内容
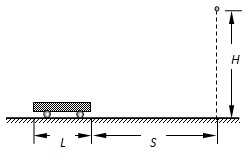 (2008?济南模拟)如图所示,质量为m的小车,静止在光滑的水平地面上,车长为L,现给小车施加一个水平向右的恒力F,使小车向右做匀加速运动,与此同时在小车的正前方S处的正上方H高处,有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),问恒力F满足什么条件小球可以落到小车上?
(2008?济南模拟)如图所示,质量为m的小车,静止在光滑的水平地面上,车长为L,现给小车施加一个水平向右的恒力F,使小车向右做匀加速运动,与此同时在小车的正前方S处的正上方H高处,有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),问恒力F满足什么条件小球可以落到小车上?分析:小球自由下落的高度一定,则下落的时间一定,小球落在小车上,则在这段时间内的位移大于s,小于(L+s),根据匀变速直线运动的位移时间公式求出小车加速度的范围,进而求出恒力范围.
解答:解:设小球的下落时间为t,则:H=
gt2
所以:t=
小球落在小车上,则在这段时间内的位移大于s,小于(L+s).
由s=
a1t2得:a1=
由L+s=
a2t2得,a2=
则
≤a≤
根据牛顿第二定律得恒力F满足
≤F≤
答:恒力F满足
≤F≤
时小球可以落到小车上.
| 1 |
| 2 |
所以:t=
|
小球落在小车上,则在这段时间内的位移大于s,小于(L+s).
由s=
| 1 |
| 2 |
| gs |
| H |
由L+s=
| 1 |
| 2 |
| g(s+L) |
| H |
则
| gs |
| H |
| g(s+L) |
| H |
根据牛顿第二定律得恒力F满足
| mgs |
| H |
| mg(s+L) |
| H |
答:恒力F满足
| mgs |
| H |
| mg(s+L) |
| H |
点评:解决本题的关键抓住小球下落的时间和小车运动的时间相等,运用匀变速直线运动位移时间公式求加速度的范围.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
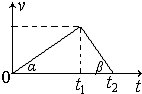 (2008?济南模拟)用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们在平均功率分别为P1和P2,则下列选项正确的是( )
(2008?济南模拟)用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们在平均功率分别为P1和P2,则下列选项正确的是( ) (2008?济南模拟)如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,则A、B两重物在运动过程中,弹簧的示数可能为:(g=10m/s2)( )
(2008?济南模拟)如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,则A、B两重物在运动过程中,弹簧的示数可能为:(g=10m/s2)( )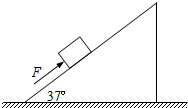 (2008?济南模拟)如图所示,重为3N的物体置于倾角为37°的斜面上,用平行于斜面的大小为5N的力F作用于物体,物体恰在斜面上做匀速直线运动,而斜面相对于地面保持静止,则下列说法中正确的是( )(cos37°=0.8,sin37°=0.6 )
(2008?济南模拟)如图所示,重为3N的物体置于倾角为37°的斜面上,用平行于斜面的大小为5N的力F作用于物体,物体恰在斜面上做匀速直线运动,而斜面相对于地面保持静止,则下列说法中正确的是( )(cos37°=0.8,sin37°=0.6 )