题目内容
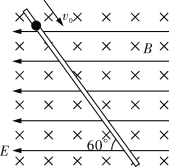
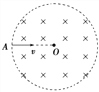
【题目】如图所示，坐标平面第Ⅰ象限内存在大小为E＝4×105 N/C、方向水平向左的匀强电场，在第Ⅱ象限内存在方向垂直纸面向里的匀强磁场．质荷比为
＝4×10－10kg/C的带正电粒子从x轴上的A点以初速度v0＝2×107m/s垂直x轴射入电场，OA＝0.2m，不计粒子的重力．求：
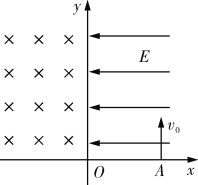
(1)粒子第一次经过y轴时，速度与y轴正方向的夹角；
(2)若要求粒子不能进入第Ⅲ象限，求磁感应强度B的最小值．(不考虑第二次进入电场后的运动情况)
【答案】(1)θ＝45° (2)
【解析】
(1)对带电粒子在电场中的运动由平抛运动规律可求出粒子速度大小与方向；
(2)设粒子在磁场中做匀速圆周运动，画出运动的轨迹，结合临界条件和向心力公式可求磁场强度.
(1)设粒子在电场中运动的时间为t，末速度与y轴正方向的夹角大小为θ，
则：
①
②
粒子经过y轴时在电场方向的分速度为：vx＝at＝2×107m/s ③
粒子经过y轴时的速度：
④
与y轴正方向的夹角大小为θ，则有：
⑤
所以θ＝45°
(2)要使粒子不进入第Ⅲ象限，如图所示，设粒子经过y轴时的位置与原点O的距离为y1，此时粒子做圆周运动的半径为R，
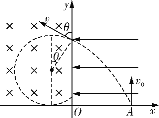
则由几何关系，
⑥
y1＝v0t ⑦
在磁场中匀速圆周运动有：
⑧
解得磁感应强度的最小值为：
练习册系列答案
相关题目
