题目内容
16.一架质量为M的直升飞机,靠螺旋桨的转动使面积为S的空气以速度v向下运动,从而使飞机悬停在空中.已知空气的密度为ρ,求速度v的大小并计算发动机的最小功率.分析 先求出△t时间内被螺旋桨加速空气的质量,根据动量定理求出螺旋桨对空气的作用力F,为使飞机停在空中,则有F=Mg,联立方程即可求解v;
由功能关系可知发动机做的功等于被加速空气的动能,据此列式即可求解功率.
解答 解:△t时间内被螺旋桨加速空气的质量为:△m=ρSv△t
螺旋桨对空气的作用力F=$\frac{△P}{△t}$
为使飞机停在空中,则有F′=F=Mg
联立求得:v=$\sqrt{\frac{Mg}{ρS}}$
发动机的最小功率:$P=F•\overline{v}$=$\frac{1}{2}Fv$
整理后知发动机的功率为:$P=\frac{Mg}{2}•\sqrt{\frac{Mg}{ρS}}$
答:速度v的大小是$\sqrt{\frac{Mg}{ρS}}$,发动机的最小功率是$\frac{Mg}{2}•\sqrt{\frac{Mg}{ρS}}$
点评 本题主要考查了动量定理、平衡条件及功能关系的直接应用,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 质量为2kg的质点在x_y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x_y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
 质量为2kg的质点在x_y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x_y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )| A. | 质点2秒末的动能为52J | |
| B. | 质点作匀变速曲线运动 | |
| C. | 质点所受的合外力为3N | |
| D. | 质点初速度的方向与合外力方向垂直 |
8.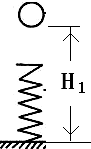 如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
 如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )| A. | v1<v2,h1=h2 | B. | v1<v2,h1<h2 | C. | v1=v2,h1<h2 | D. | v1<v2,h1>h2 |
3. 如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
 如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )| A. | 发射“嫦娥一号”的速度必须达到第二宇宙速度 | |
| B. | 在绕月圆轨道上,卫星周期与卫星质量有关 | |
| C. | 卫星受月球的引力与它到月球中心距离的平方成反比 | |
| D. | 在绕月圆轨道上,卫星受地球的引力大于受月球的引力 |
4.下列几种说法中,正确的是( )
| A. | 具有规则几何形状的物体一定是晶体 | |
| B. | 单位体积的气体分子数增加,气体的压强一定增大 | |
| C. | 满足能量守恒定律的宏观过程都可以自发地进行 | |
| D. | 露珠的形成是由于液体表面张力的作用 |
 如图所示,ABCD是柱体玻璃棱镜的横截面,其中AE⊥BD,DB⊥CB,∠DAE=30°,∠BAE=45°,∠DCB=60°,一束单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知玻璃的折射率n=1.5,求:(结果可用反三角函数表示)
如图所示,ABCD是柱体玻璃棱镜的横截面,其中AE⊥BD,DB⊥CB,∠DAE=30°,∠BAE=45°,∠DCB=60°,一束单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知玻璃的折射率n=1.5,求:(结果可用反三角函数表示)  利用气垫导轨验证机械能守恒定律时,先非常仔细地把导轨调成水平,然后依如图所示把导轨的一端垫高H,在质量为m的滑块上装上宽度为l的遮光板,使它由轨道上端任一处滑下,分别测出它通过光电门G1、G2的速度v1,v2,再测出Gl到G2的高度差h.
利用气垫导轨验证机械能守恒定律时,先非常仔细地把导轨调成水平,然后依如图所示把导轨的一端垫高H,在质量为m的滑块上装上宽度为l的遮光板,使它由轨道上端任一处滑下,分别测出它通过光电门G1、G2的速度v1,v2,再测出Gl到G2的高度差h.