题目内容
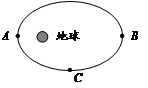
如图所示,A处为绕月轨道上运动的空间站,有一关闭动力的航天飞机在月球引力作用下向月球靠近,并与空间站在B处对接。已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中不正确的是: 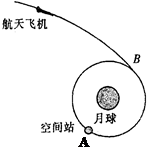
| A.图中航天飞机正加速飞向B处 |
| B.航天飞机在B处由椭圆轨道进入空间站轨道必须点火减速 |
| C.根据题中条件可以算出月球质量 |
| D.根据题中条件可以算出空间站受到月球引力的大小 |
D
解析试题分析:航天飞机在引力作用下靠近月球,引力做正功,速度增大,A正确;航天飞机在B处必须点火减速,才能与空间轨道对接,B正确;由GMm/r2=m1(2π/T)2r,根据已知条件可求出月球的质量M,C正确;空间站的质量未知,不能求出月球与空间站间的引力,D错误。
考点:本题考查万有引力定律应用。

已知地球质量为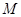 ,半径为
,半径为 ,自转周期为
,自转周期为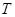 ,地球同步卫星质量为
,地球同步卫星质量为 ,引力常量为
,引力常量为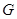 .有关同步卫星,下列表述正确的是( )
.有关同步卫星,下列表述正确的是( )
A.卫星距离地面的高度为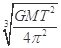 |
| B.卫星的运行速度大于第一宇宙速度 |
C.卫星运行时受到的向心力大小为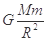 |
| D.卫星运行的向心加速度小于地球表面的重力加速度 |
美国宇航局2011年12月5日宣布,他们发现了太阳系外第一颗类似地球的、可适合居住的行星—“开普勒-22b”,它每290天环绕着一颗类似于太阳的恒星运转一周,距离地球约600光年,体积是地球的2.4倍。已知万有引力常量和地球表面的重力加速度。根据以上信息,下列推理中正确的是
| A.若能观测到该行星的轨道半径,可求出该行星所受的万有引力 |
| B.若该行星的密度与地球的密度相等,可求出该行星表面的重力加速度 |
| C.根据地球的公转周期与轨道半径,可求出该行星的轨道半径 |
| D.若已知该行星的密度和半径,可求出该行星的轨道半径 |
2008年9月25日至28日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343 km处点火加速,由椭圆轨道变成高度为343 km的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )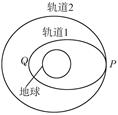
| A.飞船变轨前后的机械能相等 |
| B.飞船在圆轨道上时航天员出舱前后都处于失重状态 |
| C.飞船在此圆轨道上运动的角速度小于同步卫星运动的角速度 |
| D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 |
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨1然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1和2相切于Q点,轨道2和3相切于P点,设卫星在1轨道和3轨道正常运行的速度和加速度分别为v1、v3和a1、a3,在2轨道经过P点时的速度和加速度为v2和a2,且当卫星分别在1、2、3轨道上正常运行时周期分别为T1、T2、T3,以下说法正确的是( )
| A.v1 > v3> v2 | B.v1> v2 > v3 |
| C.a1 >a2 > a3 | D.T1 < T2 < T3 |
经长期观测人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的直径远小于两个星体之间的距离,而且双星系统一般远离其他天体。如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1:m2=3:2。则可知( )
| A.m1:m2做圆周运动的角速度之比为2:3 |
| B.m1:m2做圆周运动的线速度之比为3:2 |
C.m1做圆周运动的半径为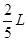 |
D.m2做圆周运动的半径为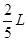 |
如图所示,行星A绕 O点沿逆时针方向做匀速圆周运动,周期为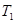 ,行星B绕 O点沿顺时针方向做匀速圆周运动,周期为
,行星B绕 O点沿顺时针方向做匀速圆周运动,周期为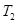 .某时刻AO、BO刚好垂直,从此时刻算起,经多长时间它们第一次相距最远( )
.某时刻AO、BO刚好垂直,从此时刻算起,经多长时间它们第一次相距最远( )
A. | B. | C. | D. |
假设地球是一半径为R、质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体的引力为零.则距地心距离为R/2处和地面处的重力加速度大小之比为( )
| A.2:1 | B.1:2 | C.4:1 | D.1:4 |