题目内容
如图所示，在半径为2a和a的同心圆围成的环状区域内存在匀强磁场，磁感应强度大小为B．质量为m、电荷量为q的带电粒子（初速度为零，不考虑重力）经加速电场加速后从A点沿半径且垂直磁场方向进入磁场，要使粒子不进入中心无磁场的圆形区域，试求：（1）带电粒子在磁场中运动的最大轨道半径
（2）加速电压的最大值．
分析：（1）粒子垂直磁场方向进入磁场后在洛伦兹力的作用下做匀速圆周运动，要使粒子不进入中心无磁场的圆形区域，则轨迹与小圆相切时，轨道半径最大，画出运动轨迹，根据几何关系求解；
（2）当半径最大时，速度最大，根据洛伦兹力提供向心力求得最大速度，根据动能定理求解最大电压．
（2）当半径最大时，速度最大，根据洛伦兹力提供向心力求得最大速度，根据动能定理求解最大电压．
解答：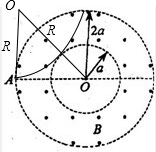
解：（1）粒子垂直磁场方向进入磁场后在洛伦兹力的作用下做匀速圆周运动，要使粒子不进入中心无磁场的圆形区域，则轨迹与小圆相切时，轨道半径最大，如图所示，
根据几何关系得：
R2+（3a）2=（R+a）2
解得：R=
a
（2）当半径最大时，速度最大，根据洛伦兹力提供向心力得：
Bqv=m
解得：v=
=
粒子加速过程中根据动能定理得：
qU=
mv2
解得：U=
答：（1）带电粒子在磁场中运动的最大轨道半径为
a；
（2）加速电压的最大值为
．
解：（1）粒子垂直磁场方向进入磁场后在洛伦兹力的作用下做匀速圆周运动，要使粒子不进入中心无磁场的圆形区域，则轨迹与小圆相切时，轨道半径最大，如图所示，根据几何关系得：
R2+（3a）2=（R+a）2
解得：R=
| 3 |
| 2 |
（2）当半径最大时，速度最大，根据洛伦兹力提供向心力得：
Bqv=m
| v2 |
| R |
解得：v=
| BqR |
| m |
| 3Bqa |
| 2m |
粒子加速过程中根据动能定理得：
qU=
| 1 |
| 2 |
解得：U=
| 9qB2a2 |
| 8m |
答：（1）带电粒子在磁场中运动的最大轨道半径为
| 3 |
| 2 |
（2）加速电压的最大值为
| 9qB2a2 |
| 8m |
点评：本题关键明确带电粒子的运动规律，画出运动轨迹，然后根据几何关系求解出半径，再根据动能定理和向心力公式求解．
练习册系列答案
相关题目
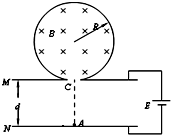如图所示，在半径为R的绝缘圆筒内有匀强磁场，方向垂直纸面向里，圆筒正下方有小孔C与平行金属板M、N相通．两板间距离为d，两板与电动势为E的电源连接，一带电量为-q、质量为m的带电粒子（重力忽略不计），在C点正下方紧靠N板的A点，无初速经电场加速后从C点进入磁场，与圆筒发生两次碰撞后从C点射出．已知带电粒子与筒壁的碰撞无电荷量的损失，且碰撞后以原速率返回．求：
（2007?西城区一模）如图所示，在半径为R，质量分布均匀的某星球表面，有一倾角为θ的斜坡．以初速度v0向斜坡水平抛出一个小球．测得经过时间t，小球垂直落在斜坡上的C点．求：
如图所示，在半径为R的水平圆盘的正上方高h处水平抛出一个小球，圆盘做匀速转动，当圆盘半径OB转到与小球水平初速度方向平行时，小球开始抛出，要使小球只与圆盘碰撞一次，且落点为B，则小球的初速度为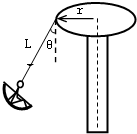
（1）在游乐场中有一种旋转飞椅，如图所示，在半径为r的平台边缘固定着长为L的绳子，另一端则是由小朋友乘坐的椅子，若绳子与竖直方向夹角为θ，当平台绕其中心轴旋转时，问：
如图所示，在半径为R=