��Ŀ����
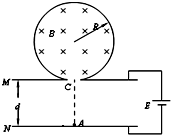 ��ͼ��ʾ���ڰ뾶ΪR�ľ�ԵԲͲ������ǿ�ų�������ֱֽ�����ԲͲ���·���С��C��ƽ�н�����M��N��ͨ����������Ϊd��������綯��ΪE�ĵ�Դ���ӣ�һ������Ϊ-q������Ϊm�Ĵ������ӣ��������Բ��ƣ�����C�����·�����N���A�㣬���پ��糡���ٺ��C�����ų�����ԲͲ����������ײ���C���������֪����������Ͳ�ڵ���ײ���������ʧ������ײ����ԭ���ʷ��أ���
��ͼ��ʾ���ڰ뾶ΪR�ľ�ԵԲͲ������ǿ�ų�������ֱֽ�����ԲͲ���·���С��C��ƽ�н�����M��N��ͨ����������Ϊd��������綯��ΪE�ĵ�Դ���ӣ�һ������Ϊ-q������Ϊm�Ĵ������ӣ��������Բ��ƣ�����C�����·�����N���A�㣬���پ��糡���ٺ��C�����ų�����ԲͲ����������ײ���C���������֪����������Ͳ�ڵ���ײ���������ʧ������ײ����ԭ���ʷ��أ�����1�����»��������˶��Ĺ켣��
��2��Ͳ�ڴų��ĴŸ�Ӧǿ�ȴ�С��
��3���������Ӵ�A���������һ�λص�A����������ʱ�䣻
��4��������������ԲͲ����N����ײ���C���������������Ӵ�A���������һ�λص�A����������ʱ�䣮
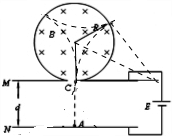
��������1�������ڴų���������Բ���˶�����ԲͲ��ֱ��ײ�أ�ÿ��Բ���켣Ϊ����֮һԲ�ܣ�
��2����ֱ���ٹ������ö��ܶ�����ʽ����Բ���˶����ٶȣ����ݼ��ι�ϵ���Բ���˶��Ĺ���뾶��Ȼ��������������ṩ��������ʽ�����Ÿ�Ӧǿ�ȣ�
��3�������˶�ѧ��ʽ�������Ӵ�A��C��ʱ�䣬Բ���˶���ʵ�ʸպ�Ϊ������ڣ���C��Aʱ����A��Cʱ����ȣ�
��4�����Ӵ�A��C�ʹ�C��A���䲻�䣬�ڴų����˶�ʱ������ܵ�Բ�ĽǺ���ʽ��⼴�ɣ�
��2����ֱ���ٹ������ö��ܶ�����ʽ����Բ���˶����ٶȣ����ݼ��ι�ϵ���Բ���˶��Ĺ���뾶��Ȼ��������������ṩ��������ʽ�����Ÿ�Ӧǿ�ȣ�
��3�������˶�ѧ��ʽ�������Ӵ�A��C��ʱ�䣬Բ���˶���ʵ�ʸպ�Ϊ������ڣ���C��Aʱ����A��Cʱ����ȣ�
��4�����Ӵ�A��C�ʹ�C��A���䲻�䣬�ڴų����˶�ʱ������ܵ�Բ�ĽǺ���ʽ��⼴�ɣ�
����⣺��1����ͼ��ʾ��
��2��������֪���������Ӵ�C���룬��Ͳ����ײ2���ٴ�C�����
��qE=
mv2
������C����ų����ڴų���������Բ���˶�������Ϊv=
��r=
����Rcot30��=
�ã�B=
��3�����Ӵ�A��C�ļ��ٶ�Ϊa=
��d=
���Ӵ�A��C��ʱ��Ϊt1=
=d
�����ڴų����˶���ʱ��Ϊt2=
=
����1����õ�Bֵ���룬��t2=��R
��ã�t=2t1+t2=
(2
d+
��R)
��4������ײn�Σ����Ӧ��һС��Բ����Բ�Ľ�Ϊ��180��-
��
��Բ���˶���ʱ��Ϊ��t2��=
T=
T=(n-1)
��
����1����õ�Bֵ���룬��t2��=��(n-1)R
���Ӵ�A��C�ļ��ٶ�Ϊa=
��d=
���Ӵ�A��C��ʱ��Ϊt1=
=d
��ã�t��=2t1��+t2=
[2
d+
(n-1)��R]
�𣺣�1�������˶��Ĺ켣��ͼ��
��2��Ͳ�ڴų��ĴŸ�Ӧǿ�ȴ�СΪ
��
��3���������Ӵ�A���������һ�λص�A����������ʱ��Ϊ
(2
d+
��R)��
��4���������Ӵ�A���������һ�λص�A����������ʱ��Ϊ
[2
d+
(n-1)��R]��

��2��������֪���������Ӵ�C���룬��Ͳ����ײ2���ٴ�C�����
��qE=
| 1 |
| 2 |
������C����ų����ڴų���������Բ���˶�������Ϊv=
|
��r=
| mv |
| qB |
| mv |
| qB |
�ã�B=
| 1 |
| R |
|
��3�����Ӵ�A��C�ļ��ٶ�Ϊa=
| qE |
| md |
a
| ||
| 2 |
���Ӵ�A��C��ʱ��Ϊt1=
|
|
�����ڴų����˶���ʱ��Ϊt2=
| T |
| 2 |
| ��m |
| qB |
����1����õ�Bֵ���룬��t2=��R
|
��ã�t=2t1+t2=
|
| 2 |
|
��4������ײn�Σ����Ӧ��һС��Բ����Բ�Ľ�Ϊ��180��-
| 360�� |
| n+1 |
��Բ���˶���ʱ��Ϊ��t2��=
(n+1)(180��-
| ||
| 360�� |
| n-1 |
| 2 |
| ��m |
| qB |
����1����õ�Bֵ���룬��t2��=��(n-1)R
|
���Ӵ�A��C�ļ��ٶ�Ϊa=
| qE |
| md |
a
| ||
| 2 |
���Ӵ�A��C��ʱ��Ϊt1=
|
|
��ã�t��=2t1��+t2=
|
| 2 |
|
�𣺣�1�������˶��Ĺ켣��ͼ��
��2��Ͳ�ڴų��ĴŸ�Ӧǿ�ȴ�СΪ
| 1 |
| R |
|
��3���������Ӵ�A���������һ�λص�A����������ʱ��Ϊ
|
| 2 |
|
��4���������Ӵ�A���������һ�λص�A����������ʱ��Ϊ
|
| 2 |
|
����������ؼ���ȷ�������ӵ��˶����ɣ������˶��켣��Ȼ����ݼ��ι�ϵ�����뾶���ٸ��ݶ��ܶ�����ţ�ٵڶ�������ʽ��⣬���⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��ʾ���ڰ뾶ΪR��Բ�������ڣ�����ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱ��Բƽ�棨δ��������һȺ�Ⱥɶ�Ϊ���ĸ�����������ͬ����v0���ϴ���P����ֽƽ������ͬ��������ų��з���ƫת���ַɳ��ų���������˵����ȷ���ǣ����������� ��������
��ͼ��ʾ���ڰ뾶ΪR��Բ�������ڣ�����ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱ��Բƽ�棨δ��������һȺ�Ⱥɶ�Ϊ���ĸ�����������ͬ����v0���ϴ���P����ֽƽ������ͬ��������ų��з���ƫת���ַɳ��ų���������˵����ȷ���ǣ����������� �������� ��ͼ��ʾ���ڰ뾶ΪR��Բ����һ�Ÿ�Ӧǿ��ΪB���������ǿ�ų���һ����Ϊm������Ϊq�����ӣ���������������A�����Բ�ķ���ֱ����ų�����C��ɳ���������˵������ȷ���ǣ�������
��ͼ��ʾ���ڰ뾶ΪR��Բ����һ�Ÿ�Ӧǿ��ΪB���������ǿ�ų���һ����Ϊm������Ϊq�����ӣ���������������A�����Բ�ķ���ֱ����ų�����C��ɳ���������˵������ȷ���ǣ������� ��2013?������ģ����ͼ��ʾ���ڰ뾶ΪR��Բ����������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱԲ�����ڣ���һ������Ϊm��������Ϊq�����ӣ���A���ذ뾶����ֱ���˴ų��ڣ��ִ�C���������AOC=120�㣬����˵����ȷ���ǣ�������
��2013?������ģ����ͼ��ʾ���ڰ뾶ΪR��Բ����������һ��ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱԲ�����ڣ���һ������Ϊm��������Ϊq�����ӣ���A���ذ뾶����ֱ���˴ų��ڣ��ִ�C���������AOC=120�㣬����˵����ȷ���ǣ������� ��ͼ��ʾ���ڰ뾶ΪR=
��ͼ��ʾ���ڰ뾶ΪR=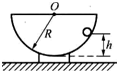 ��ͼ��ʾ���ڰ뾶ΪR�İ�Բ����Ĺ⻬�����ϣ�һ����Ϊm��С���Խ��ٶȦ���ˮƽ����������Բ���˶�����ʱ������ѹ��FN=
��ͼ��ʾ���ڰ뾶ΪR�İ�Բ����Ĺ⻬�����ϣ�һ����Ϊm��С���Խ��ٶȦ���ˮƽ����������Բ���˶�����ʱ������ѹ��FN=