题目内容
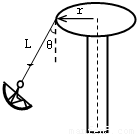
 (1)在游乐场中有一种旋转飞椅,如图所示,在半径为r的平台边缘固定着长为L的绳子,另一端则是由小朋友乘坐的椅子,若绳子与竖直方向夹角为θ,当平台绕其中心轴旋转时,问:
(1)在游乐场中有一种旋转飞椅,如图所示,在半径为r的平台边缘固定着长为L的绳子,另一端则是由小朋友乘坐的椅子,若绳子与竖直方向夹角为θ,当平台绕其中心轴旋转时,问:①若小朋友和椅子的质量共为m,则绳子的拉力为多大?
②该平台的旋转的角速度是多大?
(2)(地球质量为M,半径为r,万有引力常量为G,发射一颗绕地球表面附近做圆周运动的人造卫星,卫星的速度称为第一宇宙速度.
①试推导由上述各量表达的第一宇宙速度的计算式,要求写出推导依据.
②若已知第一宇宙速度的大小为v=7.9km/s,地球半径r=6.4×106m,万有引力恒量G=6.67×10-11 N?m2/kg2,求地球质量(结果要求二位有效数字).
分析:(1)由小朋友乘坐的椅子做匀速圆周运动,由重力和绳子的拉力提供向心力,根据牛顿第二定律,运用正交分解法求解绳子的拉力和角速度.
(2)在地球表面附近的人造卫星绕地球做匀速圆周运动时,由万有引力提供向心力,根据牛顿第二定律求出第一宇宙速度.由第一宇宙速度的计算式形变,求解地球的质量.
(2)在地球表面附近的人造卫星绕地球做匀速圆周运动时,由万有引力提供向心力,根据牛顿第二定律求出第一宇宙速度.由第一宇宙速度的计算式形变,求解地球的质量.
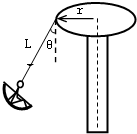
解答: 解:(1)对人和椅子整体受力分析如图,在竖直方向
解:(1)对人和椅子整体受力分析如图,在竖直方向
竖直方向有:Tcosθ=mg 得T=
水平方向:由向心力公式有
mgtanθ=mω2(r+Lsinθ)
得:ω=
(2)在地球表面附近的人造卫星绕地球做匀速圆周运动,由万有引力提供向心力,则有
G
=m
,解得 v=
(2)由上式得 M=
代入数据解得 M=6.0×1024kg
答:
(1)①若小朋友和椅子的质量共为m,绳子的拉力为
.②该平台的旋转的角速度是ω=
.
(2)①第一宇宙速度的计算式为v=
.②地球质量为6.0×1024kg.
 解:(1)对人和椅子整体受力分析如图,在竖直方向
解:(1)对人和椅子整体受力分析如图,在竖直方向竖直方向有:Tcosθ=mg 得T=
| mg |
| cosθ |
水平方向:由向心力公式有
mgtanθ=mω2(r+Lsinθ)
得:ω=
|
(2)在地球表面附近的人造卫星绕地球做匀速圆周运动,由万有引力提供向心力,则有
G
| Mm |
| r2 |
| v2 |
| r |
|
(2)由上式得 M=
| v2r |
| G |
代入数据解得 M=6.0×1024kg
答:
(1)①若小朋友和椅子的质量共为m,绳子的拉力为
| mg |
| cosθ |
|
(2)①第一宇宙速度的计算式为v=
|
点评:本题旋转飞椅和卫星都做匀速圆周运动,分析受力情况,确定向心力的来源是关键.

练习册系列答案
相关题目
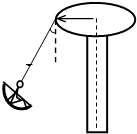 在游乐场中有一种旋转飞椅,如图所示,在半径为r的平台边缘固定着长为L的绳子,另一端则是由小朋友乘坐的椅子,若绳子与竖直方向夹角为θ,当平台绕其中心轴旋转时,问:
在游乐场中有一种旋转飞椅,如图所示,在半径为r的平台边缘固定着长为L的绳子,另一端则是由小朋友乘坐的椅子,若绳子与竖直方向夹角为θ,当平台绕其中心轴旋转时,问: