题目内容
【题目】如图所示为某研究小组设计的电磁炮供弹和发射装置。装置由倾角θ=37°的倾斜导轨和水平导轨在AB处平滑连接而成,电磁炮发射位置CD与AB相距x=0.4m。倾斜导轨处有垂直导轨平面向上的匀强磁场,磁感应强度为B1,ABCD区域无磁场,CD处及右侧有竖直向上的匀强磁场,磁感应强度为B2.倾斜导轨顶端的单刀双掷开关可连接阻值R=1.0Ω的电阻和电容C=0.5F的电容器。质量m=2.0kg、长度L=1.0m、电阻r=1.0Ω的金属杆ab代替电磁炮弹,金属杆与倾斜导轨和ABCD区域导轨之间的动摩擦因数均为μ=0.5,CD右侧导轨光滑且足够长。供弹过程:开关打到S1处,金属杆从倾斜导轨某个位置及以上任意位置由静止释放,金属杆最终都恰好精确停在CD处;发射过程:开关打到S2处,连接电压U=100V电容器,金属杆从CD位置开始向右加速发射。已知导轨间距为L=1.0m,sin37°=0.6,cos37°=0.8,不计空气阻力。
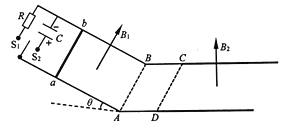
(1)求金属杆到达AB处时速度v的大小;
(2)为精确供弹,求磁感应强度B1的大小;
(3)当B2多大时,金属杆的最终速度最大?最大速度为多少?
【答案】(1)2m/s(2)2.0T(3)25m/s
【解析】
(1)金属杆从AB到CD的过程,根据动能定理得:
![]()
可得:
v=2m/s。
(2)为精确供弹,金属杆只要在倾斜导轨上最终达到匀速运动,则有:
![]()
又
F安=![]()
解得:
B1=2.0T
(3)稳定时金属杆速度最大,设金属杆的最终速度是v1,此时电容器为电压为U1,则有:
U1=B2Lv1
金属杆受到的安培力的冲量,由动量定理得:
∑B2iL△t=mv1-0
即为:
B2Lq=mv1
其中
q=C(U-U1)
联立得:
v1=![]()
当
![]() =B2L2C
=B2L2C
即得:
B2=2.0T
最大速度为:
v1=25m/s。
答:(1)2m/s(2)2.0T(3)25m/s