Question

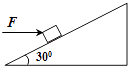
【题目】如图所示，倾角为30°的光滑斜面固定在水平地面上，质量均为m的物块A和物块B并排在斜面上，斜面底端固定着与斜面垂直的挡板P，轻弹簧一端固定在挡板上，另一端与物块A连接，A、B处于静止状态，若A、B粘连在一起，用一沿斜面向上的力FT缓慢拉物块B，当拉力FT= 时，A的位移为L；若A、B不粘连，用一沿斜面向上的恒力F作用在B上，当物块A的位移为L时，A、B恰好分离，重力加速度为g，不计空气阻力．

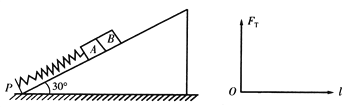
求：（1）弹簧的劲度系数和恒力F的大小；

（2）请推导FT与物块A的位移l之间的函数关系并画出FT—l图象，计算A缓慢移动L的过程中FT做功的大小；

（3）当A、B不粘连时，恒力，作用在物块B上，A、B刚分离时速度的大小.

Answer 1

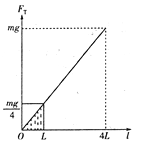
【答案】（1）； （2）如图所示， （3）

【解析】（1）设弹簧的劲度系数为k，初始A、B静止，弹簧的压缩量为x，根据平衡条件可得①

当A、B缓慢移动L时，沿斜面方向根据平衡条件可得②

联立解得③

当A、B恰好分离时二者之间的弹力为零，对A，应用牛顿第二定律可得④

对B应用牛顿第二定律可得⑤

联立解得⑥

（2）当A的位移为时，根据平衡条件有： ⑦

联立①⑦可知⑧

画出图像如图所示，

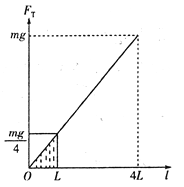
A缓慢移动位移L，图像与坐标轴所围成的面积等于做功大小，即⑨

（3）设A通过的位移为L的过程中弹力做功的大小为W，分别对两个过程应用动能定理可得：

又，联立解得