题目内容
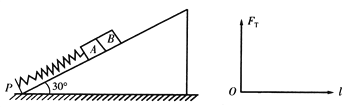
【题目】如图所示,质量为m的物体,放在一固定斜面上,当斜面倾角为30°时恰能沿斜面匀速下滑.对物体施加一大小为F的水平向右恒力,物体可沿斜面匀速向上滑行.设最大静摩擦力等于滑动摩擦力,当斜面倾角增大并超过某一临界角θ0时,不论水平恒力F多大,都不能使物体沿斜面向上滑行,试求: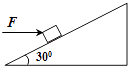
(1)物体与斜面间的动摩擦因数;
(2)这一临界角θ0的大小.
【答案】
(1)解:物体m匀速下滑时应有:mgsin30°=μmgcos30°,解得μ=tan30°= ![]() ;
;
答:物体与斜面间的动摩擦因数为μ= ![]()
(2)解:设斜面的倾角为α,对物体受力分析,由匀速运动的条件应有:
Fcosα=mgsinα+ ![]() ①
①
![]() =
= ![]() ②
②
![]() =
= ![]() ③
③
联立①②③可得F= ![]() ,讨论如下:
,讨论如下:
当cosα﹣μsinα=0时,F→∞,即无论用多大的力都不能使物体沿斜面上滑,可解得临界角tan ![]() =tanα=
=tanα= ![]() =
= ![]() ,解得
,解得 ![]() =60°
=60°
答:临界角 ![]() =60°
=60°
【解析】本题(1)的关键是正确对物体受力分析,采用正交分解法分别列出牛顿第二定律表达式,然后求解即可;题(2)的关键是根据牛顿第二定律写出物体匀速时的函数表达式,然后再讨论即可.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目