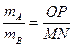题目内容
图1-1-1中(1)所示为一根竖直悬挂的不可伸长的轻绳,下端拴一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动.在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图1-1-1(2)所示.已知子弹射入的时间极短,且图1-1-1(2)中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
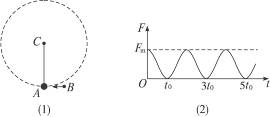
图1-1-1

图1-1-1
m=
l=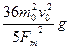
E=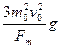

l=
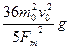
E=
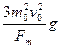
由题图(2)可直接得出,A、B一起做周期性运动,运动的周期:T=2t0 ①
令m表示A的质量,l表示绳长,v1表示B运动到最低点时的速度,v2表示运动到最高点时的速度,F1表示运动到最低点时绳的拉力,F2表示运动到最高点时绳的拉力.根据动量守恒定律,
得m0v0=(m0+m)v1 ②
在最低点和最高点处运用牛顿定律可得F1-(m+m0)g=(m+m0)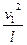 ③
③
F2+(m+m0)g=(m+m0) ④
④
根据机械能守恒定律可得2l(m+m0)g= (m+m0)v12-
(m+m0)v12- (m+m0)v22 ⑤
(m+m0)v22 ⑤
由题图(2)可知F2="0 " ⑥
F1=Fm ⑦
由以上各式可解得,反映系统性质的物理量是m= ⑧
⑧
l= ⑨
⑨
A、B一起运动过程中的守恒量是机械能E,若以最低点为势能的零点,则
E= (m+m0)v12 ⑩
(m+m0)v12 ⑩
解得E=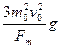 .
.
令m表示A的质量,l表示绳长,v1表示B运动到最低点时的速度,v2表示运动到最高点时的速度,F1表示运动到最低点时绳的拉力,F2表示运动到最高点时绳的拉力.根据动量守恒定律,
得m0v0=(m0+m)v1 ②
在最低点和最高点处运用牛顿定律可得F1-(m+m0)g=(m+m0)
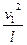 ③
③F2+(m+m0)g=(m+m0)
 ④
④根据机械能守恒定律可得2l(m+m0)g=
 (m+m0)v12-
(m+m0)v12- (m+m0)v22 ⑤
(m+m0)v22 ⑤由题图(2)可知F2="0 " ⑥
F1=Fm ⑦
由以上各式可解得,反映系统性质的物理量是m=
 ⑧
⑧l=
 ⑨
⑨A、B一起运动过程中的守恒量是机械能E,若以最低点为势能的零点,则
E=
 (m+m0)v12 ⑩
(m+m0)v12 ⑩解得E=
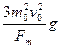 .
.
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目


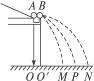
 着ml=3kg,m2=2kg的物块,两物块与小车间的动摩擦因数为μ=0.5。两物块间夹有一压缩轻质弹簧,物块间有张紧的轻绳相连。小车右端有与m2相连的锁定开关,现已锁定。水平地面光滑,物块均可视为质点。现将轻绳烧断,若己知m1相对小车滑过0.6m时从车上脱落,此时小车以速度v0=2m/s向右运动,当小车第一次与墙壁碰撞瞬间锁定开关打开。设小车与墙壁碰撞前后速度大小不变,碰撞时间极短,小车足够长。(g="10" m/s2)求:
着ml=3kg,m2=2kg的物块,两物块与小车间的动摩擦因数为μ=0.5。两物块间夹有一压缩轻质弹簧,物块间有张紧的轻绳相连。小车右端有与m2相连的锁定开关,现已锁定。水平地面光滑,物块均可视为质点。现将轻绳烧断,若己知m1相对小车滑过0.6m时从车上脱落,此时小车以速度v0=2m/s向右运动,当小车第一次与墙壁碰撞瞬间锁定开关打开。设小车与墙壁碰撞前后速度大小不变,碰撞时间极短,小车足够长。(g="10" m/s2)求:


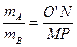 B.
B.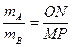
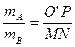 D.
D.