题目内容
【题目】如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场,磁感应强度B=1.0T,边界右侧离地面高h=0.45m处有一光滑绝缘平台,右边有一带正电的小球![]() ,质量
,质量![]() =0.1kg、电量
=0.1kg、电量![]() =0.1C,以初速度
=0.1C,以初速度![]() =0.9m/s水平向左运动,与大小相同但质量为
=0.9m/s水平向左运动,与大小相同但质量为![]() =0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后
=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后![]() 球恰好做匀速圆周运动,两球均视为质点,重力加速度
球恰好做匀速圆周运动,两球均视为质点,重力加速度![]() 。求:
。求:
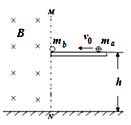
(1) ![]() 球与b球碰撞后的速度;
球与b球碰撞后的速度;
(2)碰后两球落地点间的距离。
【答案】(1)![]()
![]() (2)0.1m
(2)0.1m
【解析】
(1)a球与b球的碰撞,由动量守恒定律得:![]()
由能量守恒定律有:![]()
解得:![]()
(2)对a球,重力和电场力平衡,洛伦兹力提供向心力,
由牛顿第二定律有: ![]()
解得:![]()
设a球落地点与圆心的连线和地面夹角为![]() ,有
,有![]() ,可得:
,可得:![]()
设a球水平位移为:![]() ,
,![]()
b球不带电,碰后做平抛运动,竖直方向: ![]()
水平方向: ![]()
故两球相距:X=Xb-Xa=0.1m。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目