��Ŀ����
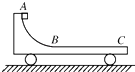
����Ŀ����ͼ��ʾ��ľ���Ҷ�BC��Ϊ ![]() �⻬Բ���Ҿ�ֹ�ڹ⻬ˮƽ���ϣ�ľ��AB�ε��ϱ�����Բ������͵����У�ľ������A��һ����Ϊ�ʵ��С���飮��ͻȻ������ˮƽ���ҵij��ٶ�v0 �� ���鵽��ľ��Bλ��ʱ�ٶȱ�Ϊԭ���ٶȵ�һ�룬֮������ϻ����պ��ܵ���Բ������ߵ�C����ľ������Ϊ2m�����������Ϊm���������ٶ�Ϊg����
�⻬Բ���Ҿ�ֹ�ڹ⻬ˮƽ���ϣ�ľ��AB�ε��ϱ�����Բ������͵����У�ľ������A��һ����Ϊ�ʵ��С���飮��ͻȻ������ˮƽ���ҵij��ٶ�v0 �� ���鵽��ľ��Bλ��ʱ�ٶȱ�Ϊԭ���ٶȵ�һ�룬֮������ϻ����պ��ܵ���Բ������ߵ�C����ľ������Ϊ2m�����������Ϊm���������ٶ�Ϊg����
��1��С���黬��Bλ��ʱľ����ٶȣ�
��2��С���鵽��Cλ��ʱ���ߵĹ�ͬ�ٶȣ�
��3���⻬Բ����İ뾶��
���𰸡�
��1���⣺����ľ�������Ϊϵͳ��ˮƽ���������������Զ����غ㣬����ٶȷ���Ϊ������
��ˮƽ�����ɶ����غ㶨�ɵã�mv0=m ![]() +2mv1��������黬��Bλ��˲��ľ����ٶ�Ϊ��v1=
+2mv1��������黬��Bλ��˲��ľ����ٶ�Ϊ��v1= ![]() v0��
v0��
��С���黬��Bλ��ʱľ����ٶȴ�СΪ ![]() v0��
v0��
��2���⣺�����鵽��Բ������ߵ�ʱ��BC�Ĺ�ͬ�ٶ�Ϊv2��������Ϊ��������ˮƽ�����ɶ����غ㶨�ɵã�
m ![]() +2m
+2m ![]() =3mv2��
=3mv2��
��ã�v2= ![]() ��
��
��С���鵽��Cλ��ʱ���ߵĹ�ͬ�ٶȴ�СΪ ![]() ��
��
��3���⣺ľ���������ɵ�ϵͳ��ֻ�������������ɻ�е���غ㶨�ɵã�
![]() m
m ![]() +
+ ![]() 2m
2m ![]() =
= ![]() 3m
3m ![]() +mgR��
+mgR��
��ã�R= ![]() ��
��
�𣺹⻬Բ����İ뾶Ϊ ![]() ��
��
����������1��������ľ����ˮƽ�������غ㣬Ӧ�ö��غ㶨�ɿ������ľ����ٶȣ���2��ľ����С������ˮƽ����ϵͳ�����غ㣬Ӧ�ö����غ㶨�ɿ���������鵽��Cʱ�Ĺ�ͬ�ٶȣ���3�������B��C����ϵͳ��е���غ㣬��ϵͳӦ�û�е���غ㶨�ɿ������Բ����İ뾶��
�����㾫�����������⣬������Ҫ�˽�ܹ�ϵ(��ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1)����Ҫ���ն����غ㶨��(�����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ���)�����֪ʶ���Ǵ���Ĺؼ���

 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�